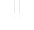Hydraulic processes in the origin of tiankengs
Palmer Arthur N. and Palmer Margaret V.
Abstract: Tiankengs are formed most commonly by the collapse of bedrock into underlying caves that contain active rivers. The collapse propagates itself by blocking and diverting the underground streams, so that hydraulic gradients become steeper and the solutional and erosional capacities are enhanced. Most of the volume of a tiankeng is produced by removal of mass by the cave streams. A large and fluctuating discharge is most favorable. As diversion passages form and enlarge, they foster further collapse and diversion. Stress release around the collapse encourages the opening of new fractures with trends that differ from regional fracture patterns. These processes account for the large scale of tiankengs in comparison to the original cave passages.
Keywords: Tiankengs, collapse, bedrock, caves, cave, active rivers, streams, hydraulic, gradients, steep, erosional, discharge, diversion passages, Stress release, fractures, trends, regional, fracture patterns, large scale, original cave passages
Introduction
Tiankengs are large karst depressions with nearly vertical walls and a mean depth and diameter typically more than 100 m each (Zhu and Zhang, 1995; Zhu and Chen, 2005). Their type area is in south-central China, where the largest and most abundant tiankengs are located (Fig. 1). Most tiankengs contain active cave streams at their bases, or show evidence that similar streams were present in the recent geologic past (Fig. 2; Senior, 1995). Although other origins are possible, collapse into cave streams must be considered the leading process of tiankeng development. This paper investigates the pertinent physical and chemical processes and provides several field examples.

Fig. 1. Dashiwei Tiankeng, Guangxi, China, is up to 613 m deep and has an opening 600 x 420 m.

Fig. 2. The downstream end of the river cave Di Feng Dong, at the base of Xiaozhai Tiankeng, Chongqing, China. The stream flow shown here is at moderate flow but represents only what is left after withdrawal of water for a hydroelectric plant. Xiaozhai is probably the world’s largest tiankeng, with a volume 1.6 times greater than that of Dashiwei Tiankeng.
Field observations
Two active field examples from the karst of southern Indiana, USA, are used here to illustrate the processes that appear to produce tiankengs. This karst area is developed on early Carboniferous limestones and dolomites with a mean dip of about 0.3° to the southwest. The carbonate rocks have been dissected to a maximum of about 50 m by through-flowing rivers, to form an extensive karst plain typified by closely clustered dolines. Both of the Indiana examples are small relative to tiankengs, but they provide easy access for viewing the essential processes.
Wesley Chapel Gulf
Lost River, with a drainage area of roughly 400 km2, is the largest stream that lies entirely within the southern Indiana karst (Malott, 1932; Bassett, 1976). The downstream half of the basin consists mainly of subsurface drainage that is partly accessible through cave entrances. Exploration and dye tracing show that the present underground paths of the water deviate considerably from the former bed of the river, which is now dry (Fig. 3).
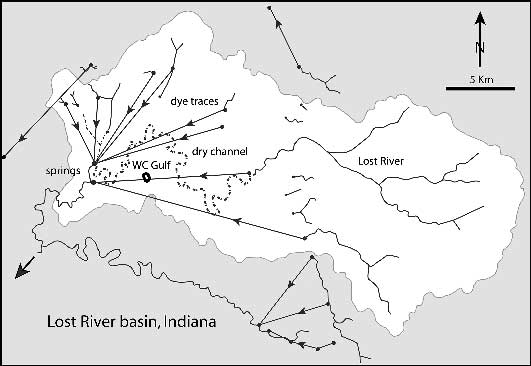
Fig. 3. Map of the Lost River basin of southern Indiana, USA, showing the location of Wesley Chapel Gulf (WC) in relation to surface drainage and dye traces (modified from Bassett, 1976).
Wesley Chapel Gulf is the largest karst depression in the basin (Fig. 4). Its walls are nearly vertical along most of its perimeter. The depression is broad, with an area of 3.4 hectares (about 300 m x 100 m), but it has only about 10 m of relief from its alluviated floor to its highest rim. No one would mistake this shallow depression for a tiankeng, but it shares many of the physical characteristics of actively forming tiankengs.
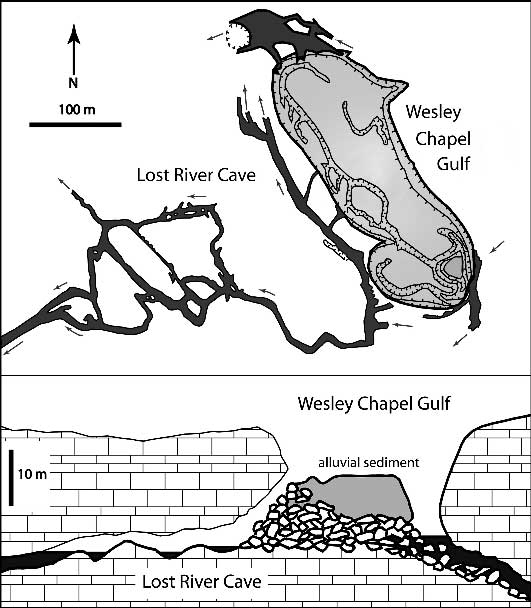
Fig. 4. Map and profile of Wesley Chapel Gulf and its related caves, from surveys by C.A. Malott (1932), updated by R.L. Powell, Indiana Geological Survey.
Three caves are accessible from entrances around the walls of the Gulf. Recent discoveries from another entrance nearby have so far accounted for more than 30 km of mapped passages, all of which lie no more than 20-30 m below the land surface. This system extends westward from Wesley Chapel Gulf for several kilometres. The Gulf and surrounding caves are located near the contact of two thin-bedded limestones, the cherty St. Louis Limestone and the overlying purer Ste. Genevieve Limestone. Collapse blocks are typically thin slabs.
The discharge through and around Wesley Chapel Gulf varies from about 0.3 to 4 m3/sec (extrapolated from data by Bassett, 1976). During low flow, water drains around and beneath the Gulf without appearing at the surface. During high flow the Gulf is flooded, and that is the source of the thick alluvium that covers its rather flat floor. The Gulf therefore has the geomorphic character of a polje, but without the size or the structural guidance that is typical of poljes. As cave development progresses, the Gulf widens by collapse around its perimeter. This collapse in turn forces the water to seek alternate routes, which perpetuates the tendency for further collapse. The entire Lost River Cave consists of multiple routes for water with many overflow passages formed by periodic floodwaters. Accessible cave passages are generally less than 10 m in width and height (Fig. 5), and it is clear that collapse of a single passage could not produce a depression as broad as Wesley Chapel Gulf.

Fig. 5. One of the main stream passages in Lost River Cave during low flow.
Blue Spring Cave
The processes that operate at Wesley Chapel Gulf are even more clearly revealed at Blue Spring Cave, 18-20 km to the north (Fig. 6). This cave is a large dendritic stream system with a total of 34 km of mapped passages. It is located mainly in the massive, prominently jointed Salem Limestone, which produces large collapse blocks instead of thin slabs. It is overlain by the thin-bedded, cherty and shaly lower strata of the St. Louis Limestone. The main stream has a maximum discharge of more than 10 m3/sec and a minimum of only about 0.1 m3/sec (measurements by the authors). The cave drains an area of about 30 km2.
Fig. 6. Map of Blue Spring Cave, Indiana. The shaded area shows the location of a maze of diversion passages around an extensive collapse zone. (Map by A. Palmer, D. Chase, M. Palmer, T. Hall and others.).
As the cave enlarged, the main stream passage collapsed at a junction with a major tributary, to form a large compound doline (Fig. 7). The main passage in this area has a width and height of about 10 m, and the land surface lies an average of 20-25 m above the passage ceiling. The collapse material has a low enough permeability that it eventually forced both the main stream and its tributary to develop alternate routes around it. The sequence of collapse and diversion is clearer than at Wesley Chapel Gulf, but the surface depression is much smaller and has no flat floor.
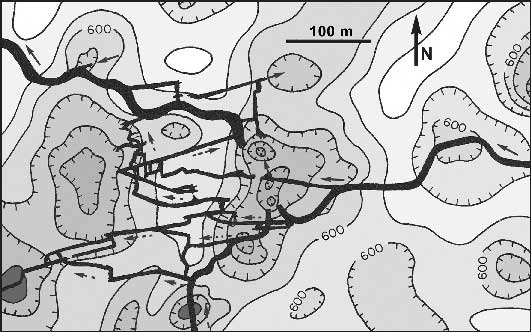
Fig.7. Map of the Maze, Blue Spring Cave, and its relation to compound dolines at the surface. Cave passages are delineated with black lines. The shaded areas are depressions and the dark gray areas are doline ponds. Arrows indicate flow directions in the cave. The main stream enters from the right and exits at upper left. The major tributary enters from the bottom of the map. The major collapse is located beneath the line of deepest dolines in the middle of the map. Contours are in feet (600 ft = 183 m) and the contour interval is 10 feet (= 3 m).
The diversion routes now form a labyrinth of passages, known as the Maze, which has a total length of about 1.5 km (Fig. 8). Nearly all of these passages are joint-guided fissures in the Salem Limestone. The total relief in the Maze is about 20 m, about half of which lies below the present water table. Its passages have irregular ceiling heights and contain pools up to 10 m deep. Today the entire combined flow of the main cave stream and its tributary passes through the Maze. Its passages are small enough that water fills them entirely during severe floods, so they continue to grow and multiply.

Fig. 8. A passage in the Maze of Blue Spring Cave during low flow.
The orientation of solution facets (scallops) in the walls of the Maze show that some of the water has traveled through the breakdown as well as around it on both sides. Water from the main stream now bypasses the collapse around the northeastern side, while water from the tributary follows southwesterly bypass routes. The passage pattern shows that originally most of the flow from the main stream also drained around the southwestern side. The collapse and diversion appears to date from the late Pleistocene at least 100,000 years ago. This estimate is based on dating of correlative passages in other caves, including Mammoth Cave, Kentucky, 175 km to the south in an extension of the same karst area (Granger et al, 2001).
As shown in Figure 7, the deepest dolines overlie the collapse in the main cave passage, but many of the shallower ones seem to show no relation to the passages beneath. The thin-bedded St. Louis Limestone tends to provide lateral paths for vadose water, in preference to vertical paths. Many dolines in the St. Louis are enlarged by the removal of material to points where the water is able to descend vertically into the underlying Salem Limestone. In addition, some dolines have formed over secondary collapse zones in and around the Maze.
The Salem Limestone contains two prominent joint sets with average trends about 10° counterclockwise from east-west and north-south. These trends are roughly parallel to the regional dip and strike. The local dip direction and angle vary throughout the cave but have no apparent effect on the joint patterns. The overall passage orientation in the cave follows the same pattern as the joints. More than half of the passage length is guided by the dip-oriented joints, and a much smaller percentage follows the strike-oriented joints. These trends are shown in the rose diagram of individual passage segments, obtained from the survey data for the entire cave and weighted by length (Fig. 9). However, if only the passages in the Maze are considered, a different pattern emerges. In the Maze, much of the passage length has the same trends as those in the rest of the cave, but even greater lengths are oriented at angles about 15-25° to either side of the dip-oriented trend. As a result, many passage segments in the Maze intersect at conspicuously acute and obtuse angles.
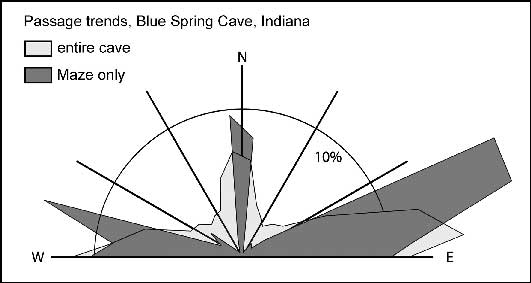
Fig. 9. Rose diagram comparing passage trends in the Maze with those in the entire Blue Spring Cave. The lengths in each sector are summations of the lengths for each passage segment in the survey data.
There are two possibilities for the difference in passage trends between the Maze and the rest of the cave. It is most likely that stresses in the vicinity of the collapse have produced additional joints with trends that are not present elsewhere. A less plausible explanation is that the diversion passages simply follow existing joints that were not utilized by the main passages until they could be enlarged by stress release around the collapse. The “new” joints are roughly radial and tangential to the main collapse zone, which suggests that the directions of most of the Maze passages are related to stress patterns produced directly by the collapse. Development of new joints can be important in aiding the diversion of cave streams around collapse zones. If similar stresses are present around the collapses that form tiankengs, the resulting fractures may help to define some of the vertical walls of these depressions.
Genetic processes
The dolines described above have an origin that involves not only bedrock collapse, but also hydraulic processes, dissolution, and erosion. Most of these processes can be quantified, which helps to support the concepts and also to show that the observations of small dolines apply as well at the huge scale of tiankengs.
Nature of bedrock collapse
The largest tiankengs have a much greater volume than any known cave room. To account for the large mass of material that has been removed from a tiankeng, much more than collapse into a single cave passage is required. Collapse of a cave produces a jumble of rock that occupies about 20-40% more volume than the original opening. As the collapse propagates upward, the blocks eventually fill the available space so that further collapse is greatly diminished or halted entirely (Šušteršič, 1984). In the breakdown pile in Figure 10, note the loose packing of the upper blocks and the proximity of the intact ceiling above them. If only a few ceiling blocks fall into a cave, there is no change in overall cross-sectional area. Space is neither created nor filled, but is simply redistributed. There is greater resistance to underground stream flow because the openings are smaller than the original passage. If bedrock collapse is the only active process, even if it extends all the way to the surface, any resulting karst depression would be considerably smaller than the original collapsed cave.

Fig. 10. Collapse at a passage intersection in Mammoth Cave, Kentucky. The strata are similar in age and character to those in Lost River Cave.
If the collapse continues and the cave ceiling migrates upward, eventually the top of the breakdown pile may become inaccessible even to floodwaters. As a result, the only space available for the stream flow is the lower sections of the breakdown pile. This part of the pile has the lowest permeability, because small breakdown fragments tend to filter down between the larger blocks and fill much of the space. Shaly beds tend to crumble into small chips that can clog the openings between blocks of more competent bedrock. Sediment and soil from the surface may contribute to the pore filling. If material is removed from the bottom of the pile by erosion and dissolution, much of the space is re-filled by material subsiding from above. The size of the surface depression depends almost entirely on the volume of material carried away by the cave stream.
Hydraulic processes
As collapse material accumulates in a cave, the hydraulic efficiency is reduced considerably. A steeper hydraulic gradient is required to transmit water through a collapse zone than through the original unobstructed passage, and therefore the water tends to pond at the upstream side of the obstruction to provide the necessary gradient.
The amount of hydraulic head that is lost across a constriction in a water-filled cave passage is illustrated in Figure 11. In this figure the constriction is simplified to a single narrow tube that interrupts the main passage. The total head loss through the narrow tube is shown in relation to the discharge and to the ratio of passage diameters. The hydraulic gradient in the unobstructed passage is very small compared to that in the narrow tube. The total head loss (Δh) across the constriction is shown on the left axis of the graph. This is how high the water would have to rise at the upstream end of the constriction to allow the water to pass through. But since the entire passage is already water-filled, Δh would be represented as pressure head, which is the height to which water would rise in a well that penetrates the cave passage.
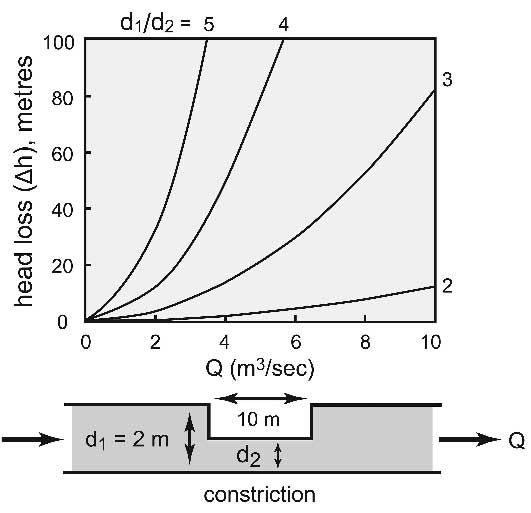
Fig. 11. Head loss across a constriction in a cave passage, in relation to discharge and ratio of passage diameters.
For example, if the passage diameter constricts from 2 m to 0.5 m, d1/d2 = 4. If the discharge (Q) = 3 cubic metres per second, the head would rise almost 30 m higher at the upstream end of the constriction than at the downstream end. Such steep gradients are only intermittent, as they are likely to occur only during large floods. It is during those times that the water would be most likely to form bypass routes through the network of joints and partings around the constriction.
The head loss caused by the constriction is composed of several parts: the line loss, which is the head difference that is necessary to move the water through the narrow tube, and the local losses, which represent the head consumed by changes in velocity (either magnitude or flow direction). Local losses occur at any convergence, divergence, bend, obstruction, or junction. The line loss is computed by
Δhline = (v2 f L) / (2 d g)
where v = mean flow velocity, f = friction factor, L = flow distance, d = passage diameter, and g = gravitational field strength. Any compatible system of units may be used. The friction factor (f), which has no units, is about 0.03-0.05 in a typical cave passage. Reports of field measurements in caves often cite f values as high as 100, but these include all the local losses, including those caused by breakdown. This equation can be modified for non-circular cross sections, but the details are unnecessary here.
Local head losses are all proportional to v2. They must be computed with the aid of experimental coefficients, which can be found in most books on fluid mechanics. Local head losses can also be estimated from changes in momentum, which means that any change in velocity (due either to variations in cross-sectional area or to curvature of flow) will contribute to the local head loss. Local head losses in Figure 11 are caused only by convergence of water into the narrow tube and divergence at the end of the tube. During high flow, these may exceed the line loss. No coefficients are available for cave breakdown, but the concept of head loss by itself is sufficient for geological interpretation. When one considers the many constrictions, enlargements, branches, and curves that the water must negotiate in a breakdown pile, it is obvious that the head loss will be much greater than that shown in Figure 11.
Because all head losses increase with the square of the flow velocity, hydraulic gradients are steepest during floods, especially in constrictions where the cross-sectional area is small. During low flow, a cave stream may be able to pass easily through a breakdown pile. But during floods, when the discharge is at least hundreds of times greater, the water will pond severely on the upstream side of the breakdown pile. This imposes a high pressure on the surrounding bedrock, and a steep hydraulic gradient across the boulder pile and any openings that bypass it. Enlargement of diversion passages around the breakdown is most rapid at these times.
Dissolution rates
When water ponds upstream from a collapse or other passage constriction, considerable pressure can build up (Fig. 11). Aggressive water from the cave is forced into all available openings in the surrounding bedrock, which rapidly forms a network of enlarged fissures. Because of the steep hydraulic gradient, there is a tendency for many of these openings to bypass the constriction.
Consider the system of bypass routes where Q = discharge (cm3/sec), b = long dimension of the fissure cross section (cm), and L = fissure length (cm). Most such fissures are short, with fairly large initial widths. A fissure in limestone with Q/bL > 0.001 cm/sec will enlarge at the maximum possible rate allowed by the water chemistry (Palmer, 1991). All fissures that exceed this value will enlarge at roughly equal rates. For reference, consider a typical fissure where b = 100 cm and L = 10,000 cm. A discharge (Q) of 1 L/sec is needed for it to reach the maximum enlargement rate. This may not be achieved during low flow, but during periodic floods a large number of fissures could sustain this amount of discharge. The result is a maze of interconnecting passages in which all fissures enlarge at roughly uniform rates of about 0.001-0.1 cm/yr, depending on the water chemistry. The amount of annual growth also depends on how long the floodwater conditions persist during the year. Even where new passages are not formed, the stream will dissolve the breakdown blocks and allow more to come down from above. For further discussion, see Palmer (1991, 2002).
To achieve high dissolution rates at and around the collapse zone, cave water must arrive while still considerably undersaturated with the local carbonate minerals. Field measurements show that the degrees of calcite and dolomite saturation almost invariably decrease with increasing discharge (see example in Fig. 12). In many cave streams the low-flow water is supersaturated, owing to loss of carbon dioxide to the surface through cave entrances and smaller openings. Even in these caves, the water becomes aggressive during floods and retains low saturation levels for long distances into the aquifer (Palmer, 2002).
The negative slope of SI vs. stage in Figure 12 is typical of cave streams. From this relationship it is possible to show that the dissolution rate varies with at least the second power of the flow velocity. However, this single field example does not apply everywhere. Nevertheless, the impact of periodic flooding on dissolution rate is clear.
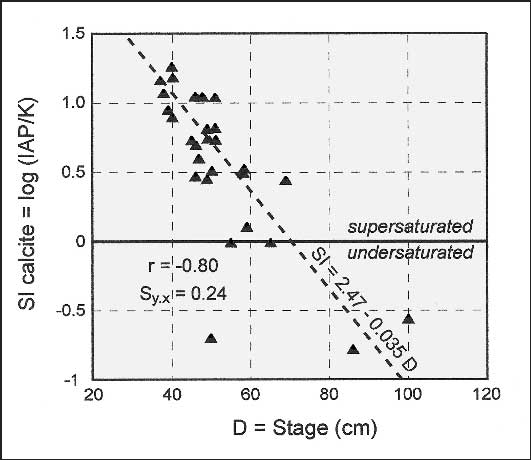
Fig. 12. Saturation index (SI) vs. flow stage in a sinking stream entering Mystery Cave, Minnesota, USA (calculated from data by S R Grow). Aggressiveness toward calcite (negative SI) is greatest during the highest flow. IAP = ion activity product, (Ca2+)(CO32-), and K = equilibrium constant (solubility product) for calcite.
Erosion rates
The erosive force (F) on an object exposed to a turbulent stream = Cd ρ v2A/2, where ρ = water density, v = water velocity, A = cross-sectional area of the object perpendicular to the flow, and Cd = drag coefficient (experimental). For a typical rectangular breakdown block with a flat side facing into the flow, Cd ~1.2. The dependence of F on v2 is similar to that of head loss in turbulent flow.
As shown by small scallop lengths, flow velocities of several metres per second are common in cave passages during floods (see Curl, 1974). A scallop length of one centimetre (a typical minimum in most passages) indicates a flow velocity of roughly 3.5 m/sec. The effective weight of a limestone block immersed in water is about 62% of its weight in air. The drag force exerted by water moving at 3.5 m/sec (about 1200 newtons) would equal the effective weight of an immersed cube of limestone of about 45 cm on each side. It is likely that this force could move the block even uphill (depending on its position relative to other blocks). Figure 13 shows blocks of sandstone more than a cubic metre in volume that have been lifted up steep slopes by floodwaters.
During low flow the drag force is a tiny fraction of what it is during floods, and little erosion can take place. The resistance of a block to erosion is also greater if it is not totally immersed in water, or if it is weighed down by other blocks. Thus, in a breakdown pile, mechanical removal of the debris in a collapse pile takes place mainly during the greatest floods.

Fig. 13. Sandstone boulders carried uphill by floodwaters in Lockridge Aqua Cave, Virginia, USA.
Conclusion
A tiankeng evolves in several stages: (1) underground diversion of a large surface river to form a cave; (2) localized collapse of the main stream passage; (3) increasing hydraulic gradients and flow velocities through the collapse material; (4) accelerated dissolution and erosion of the collapse material, especially during floods; (5) development of floodwater bypass routes; and (6) additional collapse, not only where breakdown blocks have been removed by dissolution, but also into the growing network of diversion passages. Stage 6 leads back to stage 3 in a continuing loop.
Even where the cave at the base of a tiankeng shows no evidence for multiple branches, it is likely that most of the area directly beneath the depression has been affected by development of diversion channels and collapse into them. These processes probably account for the large floor areas of tiankengs.
The origin of diversion passages is aided by the opening of fractures, both old and new, as the result of stress release during collapse. New fractures can form that have trends different from those elsewhere in the region.
When a cave stream is obstructed by collapse, the hydraulic head at the upstream end rises with the square of the flow velocity. The erosive force increases in the same way. Dissolution rates in cave streams also vary strongly with velocity. All of these processes are therefore highly sensitive to discharge. The large volume of a tiankeng therefore depends strongly on the accelerated dissolution and erosion during floods.
Acknowledgements
We wish to thank Profs. Zhu Xuewen, Liu Zaihua, and Chen Weihai of the Institute of Karst Geology, Guilin, for introducing us to the tiankengs of China, and to Dr Tony Waltham and Andy Eavis for supplying additional information. We also thank Dr. Richard L. Powell of the Indiana Geological Survey for being a mentor to our early studies of the Indiana karst.
References
- Bassett, J, 1976. Hydrology and geochemistry of the upper Lost River drainage basin, Indiana. National Speleological Society Bulletin, 38(4), 79-87.
- Curl, R L, 1974. Deducing flow velocity in cave conduits from scallops. National Speleological Society Bulletin, 36(2), 1-5.
- Granger, D E , Fabel, D, and Palmer, A N, 2001. Pliocene-Pleistocene incision of the Green River, Kentucky, determined from radioactive decay of cosmogenic 26Al and 10Be in Mammoth Cave sediments. Geological Society of America Bulletin, 113(7), 825-836.
- Malott, C A, 1932. Lost River at Wesley Chapel Gulf, Orange County, Indiana. Proceedings of Indiana Academy of Science, 41, 285-316.
- Palmer, A N, 1991. Origin and morphology of limestone caves. Geological Society of America Bulletin, 103, 1-21.
- Palmer, A N, 2001. Dynamics of cave development by allogenic water. Acta Carsologica, 30(2), 13-32.
- Senior, K J, 1995. The Yangtze Gorges Expedition: China Caves Project 1994. Cave and Karst Science, 22, 53-90.
- Šušteršič, F, 1984. A simple model of the collapse doline transformation. Acta Carsologica, 12, 107-138.
- Zhu X and Zhang Y, 1995. The world’s largest dolines and Great Crack Gorge in southern Sichuan. Carsologica Sinica, 14 (Supplement), 1-11.