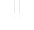Baudouin Lismonde
Limestone wall retreat in a ceiling cupola controlled by hydrothermal degassing with wall condensation ( Szunyogh model) ( Comments to Wolfgang Dreybrodt remark "On feasibility of condensation processes in caves", Speleogenesis and Evolution of Karst Aquifers, 1 (2), 2003, www.speleogenesis.net )
Audra, Bigot and Mocochain (2003) proposed an explanation for the development of a hydrothermal cave in Provence ( France ), referring to the Szunyogh model (1989). Dreybrodt (2003) then shows by calculations that this model is unlikely. We will discuss Dreybrodt's answer here. Our conclusions will emphasise that Dreybrodt's hypothesis (transient conduction in a semi-infinite solid) is not the only possibility. When other conditions are considered (steady-state conduction with constant temperature at a finite distance), this cupola-development model can be valid.
W. Dreybrodt calculation
The corrosion mechanism by degassing of thermal water and condensation on the ceiling supposes, as Dreybrodt mentioned, a wall-cooling process (condensation <=> Watt's cold wall). In order to test the model proposed by Audra et al. (2003), Dreybrodt stated the implicit hypothesis that cooling proceeds in an infinite limestone mass around the ceiling cupola. This allows him to use a classical analytical solution (transient conduction in a cylindrical infinite mass). The flux at the wall diminishes approximately according to the square root of time and this flux rapidly becomes too weak to produce any noticeable condensation. Thus, the process gradually stops and the amount of limestone corrosion is too small to validate the development of cupolas.
Choice of boundary conditions. This calculation is perfectly correct. However, it is based on the hypothesis that the limestone host rock is, at the start of the process, in a steady isothermal state, meaning that the heat sink is located in an infinite distance from the cupola. In real karst this never occurs. If the ceiling cupola is located at a moderate distance below the ground surface and in a karst massif, it is normal for seepage from rainfall to occur rather close to the hydrothermal flow. This seepage water provides a source of cooling at a moderate distance from the cupola. The difference ?T between hydrothermal and meteoric seepage temperatures, at any distance ?x between both flows, generates a temperature gradient ?T/?x, which can be chosen at about 1°C/m.
New calculation with generation of low temperatures at a finite distance
One can reiterate Dreybrodt's calculation, using the same numerical data, to assess the cupola's wall retreat by degassing-condensation process.
If the heat flux remains constant with time, the total mass of condensed water (per square metre of the cupola's surface) then increases linearly with time and can be written as follows (M in kg.m -2 ):
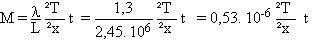
With the same value of pCO 2 as Dreybrodt, on e can obtain the depth of wall retreat D. One can show that the amount D of corroded limestone is proportional to the condensed water mass.
One can rewrite Dreybrodt's relations in SI units (M in kg.m -2 , t in s, D in m):

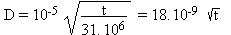
Provided that D is proportional to M, one can obtain the equivalent expression (M in kg.m -2 , D in m):
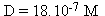
Then back to our new hypothesis:
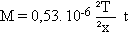
The amount of dissolved limestone is (D in m and t in s):
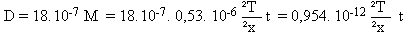
If one wishes to write D in m and t in years, one can obtain the following new relation:
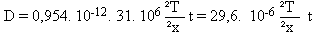
Let V be the corrosion speed (V in µm/year):
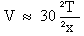
Numerical example: if the process prevails for 10 000 years with a thermal gradient ?T/?x = 3 °C/m, one obtains a wall retreat corresponding to 0.9 m. Admittedly, this is a small amount, but a larger amount can be obtained with a higher thermal gradient or a longer duration.
Conclusion
The mechanism of wall retreat by corrosion linked to CO 2 degassing and water condensation is only possible providing the existence of a seepage flow close to the hydrothermal flow, which can maintain a sufficient thermal gradient over time.
The validity of Szunyogh's theory under these conditions has already been mentioned (Lismonde 2002, p. 292). Such a process also occurs in Movile cave ( Romania ), with values one order of magnitude lower as in our calculation. Condensation corrosion was demonstrated here using stable isotopes (Sarbu and Lascu 2001)
Acknowledgment
The author thanks A. N. Palmer for his comments and for smoothing the English.
References
- Audra Ph., Bigot J.-Y. and Mocochain L. 2003. Hypogenic caves in Provence ( France ): specific features and sediments. Speleogenesis and Evolution of Karst Aquifers 1 (1), ( http://www.speleogenesis.net/archive/publication.php?PubID=9&Type=publication )
- Dreybrodt W. 2003. On feasibility of condensation processes in caves (comment to the paper Specific features and sediments). Speleogenesis and Evolution of Karst Aquifers 1 (2), ( http://www.speleogenesis.net/archive/sg2/Dreybrodt/index.htm )
- Lismonde B. 2002. Climatologie du monde souterrain, vol. 2 (Aérologie des systèmes karstiques). Comité départemental de spéléologie de l'Isère, Grenoble .
- Sarbu S. M. and Lascu Ch. 1997. Condensation corrosion in Movile cave, Romania . Journal of Cave and Karst Studies 59 (3), 99-102.
- Szunyogh G. 1989. Theoretical investigation of the development of spheroidal niches of thermal water origin. Second approximation.10 th Intern.Congress of speleology - Budapest , Hungary , III, 10, 766-768.