White W.B. and White E.L.

Abstract: Calculations are presented to show the relative contribution of the matrix, fracture, and conduit permeability to the overall flow of ground water through a karst aquifer. The conceptual model is a cross-section spanning the full width and thickness of the aquifer. A constant, but adjustable head is assumed. The rock matrix is characterized by an adjustable hydraulic conductivity. Varying proportions of fractures and conduits of adjustable fracture apertures and conduit diameters were the calculational parameters. Calculations used Darcy?s law for matrix flow, the cube law for fracture flow, and the Darcy-Weisbach equation for conduit flow. The results show a surprising dominance of fracture flow in the early stages of aquifer development. A focusing mechanism is needed to localize the flow into a relatively small number of conduits.

Keywords: ground water, aquifer, triple permeability, speleogenesis.

Introduction

Attempts to describe, analyze, or model ground water flow in karstic carbonate aquifers usually begin with some aspect of the triple permeability model (White, 1999; Worthington et al., 2000; White, 2002). The three components are matrix permeability, fracture permeability, and conduit permeability. Each contributes to the flow field but frequently only one or at most two of these components are included in the calculations. The choice of components and decisions concerning what can be neglected are often based on little more than guesswork.

The object of the present paper is to show the relative contribution of each of these permeability components to the overall flux of moving ground water. The calculations are based on a cross-section spanning the full width and thickness of the aquifer. By varying the contributions of each of the permeability components a measure of their relative importance to the overall flow system is obtained. The intent is not to provide an aquifer model, but rather, by using actual numerical values, provide some insight into when and under what circumstances, one or more of the components of aquifer permeability can be neglected. Such calculations provide some constraints on the various equivalent porous media models such as the one developed for the Edwards aquifer in Texas (Scanlon et al., 2003).

The triple permeability concept

Table 1 gives the essential characteristics of the three components of the triple permeability model for karst aquifers. The matrix, fracture, and conduit permeability are, essentially, independent components. Any specific real aquifer will have a mix of these contributions. There also exist real aquifers in which one of the components is completely dominant.

Table 1

Characteristics of the three components of the triple permeability model.

Calculations

The framework used for the calculations is shown in Fig. 1. A fixed cross-section of aquifer is assumed. The aquifer is taken as rectangular, 100 meters thick and one kilometer wide, giving a cross-sectional area of 105 m2. The aquifer cross-section is an adjustable boundary and can be set to any value, providing that the area is large compared to solution features that are embedded in it. The head is assumed to be constant and uniform across the aquifer area. This is an extreme assumption but one that eliminates concern for the water table and also the variable heads that would be characteristic of most aquifers containing conduits. The rock matrix is characterized by an adjustable hydraulic conductivity. Varying proportions of fractures and conduits of adjustable fracture apertures and conduit diameters are the calculational parameters. A further assumption is that there is sufficient recharge behind the aquifer cross-section to provide whatever flow is called for by the calculations.

The guiding equations for the permeability (Table 1) show that the flow rate, Q, varies linearly with the head in laminar flow but with the square root of the head in turbulent flow. The head becomes a scaling variable. The head, or hydraulic gradient, dh/dL, is here set equal to 0.01, a nominal value for small karstic drainage basins. The guiding equations contain the density and viscosity of water, both of which are functions of temperature. A temperature of 10 ˚C was selected as typical of karst ground waters but the variation in the parameters over the range of temperatures expected in karst aquifers is relatively small.

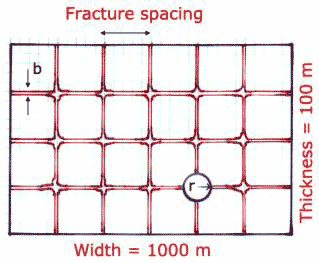
Fig. 1. Sketch showing the aquifer cross-section used for calculations.

The matrix component

Ground water flow through the limestone or dolomite bedrock is not intrinsically different from ground water flow in any other aquifer. The guiding equation is Darcy?s law. However, calculations must use hydraulic conductivities for the rock. Such data are sparse. Most hydraulic conductivities are based on pump tests on wells and those data are dominated by the fracture flow component. Intrinsic hydraulic conductivities of the bulk rock must be measured on core samples in the laboratory. Some representative data are shown in Table 2.

The flux through the matrix is a fixed quantity for chosen values of hydraulic conductivity. Lines of constant flow rate were calculated for Kentucky Mississippian limestone (K = 2 x 10-11 m/sec) which should be typical of many Paleozoic limestones and dolomites. Other lines of constant flow were calculated for the Edwards Limestone (K = 1 x 10-8 m/sec) and for the mean value of the Floridan aquifer (K = 3.65 x 10-6 m/sec). The latter is a carbonate aquifer in which matrix flow is a dominant component.

Table 2

Hydraulic conductivities for some carbonate rock aquifers

The fracture component

The idealized model for fracture flow assumes a fracture with plane parallel walls and a uniform aperture. For the ideal case, the cubic law can be derived theoretically from the Navier-Stokes equations.

[1]

Here, Q = flow rate in m3/sec, w = fracture width in m, ρ = density of water = 999.7 kg/m3, g = gravitational acceleration = 9.8 m/sec2, b = full aperture of the fracture in m, and η = viscosity of water = 1.307 x 10-3 Pa sec.

It has been long recognized that real fractures do not have uniform apertures and that the walls are not parallel. Witherspoon et al. (1980) resolved this problem by compacting the constants of equation [1] into a single constant and then adding an empirical friction factor, f, to give the form of the equation shown in Table 1. More recent work (e.g. Brush and Thomson, 2003; Konzuk and Kueper, 2004) has proposed more quantitative descriptions of rough-walled fractures but in general the results change by no more than a factor of 2. For the rough calculations in this paper, the plane-walled fracture (equation [1]) should suffice.

The fracture width, w is the total extent of fractures measured perpendicular to the flow direction. There may be multiple fracture sets at different angles with respect to each other. In the model assumed in Fig. 1, there are both vertical fractures and horizontal bedding plane partings in an assumed horizontal bedding. The total width of vertical fractures is the aquifer width/mean fracture spacing. The total width of horizontal fractures is the aquifer thickness/mean spacing of bedding plane partings. With the aquifer dimensions given in Fig. 1 and a typical 10 meter spacing for both vertical fractures and bedding plane partings, the model would contain 18,900 meters of fracture assuming that the boundary planes are not fractures. A second curve was calculated using only vertical fractures with a 50 m spacing.

Fracture flow calculations were cut off when the aperture reached 0.01 m as this is the dimension at which turbulent flow is expected to develop. The cubic equation applies only to laminar flow. If all fractures were to develop to the largest aperture, fracture flow would completely dominate the flow system. Something like this occurs in aquifers with maze cave development. In most aquifers, rearrangements of the flow path would have occurred before all of the fractures reached this very large aperture.

The conduit component

A single conduit is assumed as sketched in Fig. 1. The conduit radius, r, is taken as the dependent variable. Conduit flow in the laminar regime is described by the Hagen-Poiseuille equation [2].

[2]

Turbulent flow in a conduit is described by the Darcy-Weisbach equation. Written as volume flow and taking the cross-section as a circular conduit gives

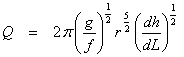[3]

Application of equation [3] requires numerical values for the Darcy-Weisbach friction factor, f, which must be determined empirically. The friction factor relates to the wall roughness and, in the case of a conduit that behaves as a uniform pipe, estimates of f have been made from irregularities, usually scallops, on the conduit wall. Most conduits, however, are not uniform pipes. Breakdown, sediment chokes, and varying passage shapes also contribute to the effective roughness. An alternative approach is to measure all other parameters in equation [3] and then back calculate f. The two approaches give dramatically different results as shown in Table 3. Because the friction factor enters the Darcy-Weisbach equation as a square root, the effect of the different numerical values is somewhat muted. Calculations were made with the smallest value (0.039) and one of the largest values (130).

Table 3

Estimates of the Darcy-Weisbach friction factor

Discussion and conclusions

The results of all calculations are plotted in Fig. 2. The x-axis gives the aperture, either fracture aperture or conduit radius. The y-axis shows the flow volume that would be expected under the specified conditions of aquifer cross-section and hydraulic head. Changing the aquifer cross-section and the hydraulic head would shift the numerical positions of the curves but not their relative pattern.

For matrix flow the ?aperture? is the total cross-section of the aquifer so the matrix components plot as horizontal straight lines whose vertical position depends only on the assumed hydraulic conductivity. As expected, in the dense, low permeability Paleozoic limestones, the matrix flow is negligible. It becomes more important in more permeable limestones and yields a significant contribution to the flow field when K exceeds values of 10-6 m/sec.

A surprise in the calculations is the dominance of fracture flow. Most observed fractures in carbonate aquifers have apertures in the range of hundreds of micrometers. If these fractures were enlarged by dissolution to the millimeter to centimeter range, fracture flow would completely dominate the system. What happens in most aquifers is the focus of the flow into a few localized pathways early in the development of the system. Because of the acceleration of dissolution kinetics at the critical aperture in the one-centimeter size range, a single conduit or small set of conduits grow at the expense of near by fractures. Lowering hydraulic heads in the conduits cause the conduits to act as drains and the simplified model used for the present calculations is not applicable. In those aquifers where geologic factors prevent the focus of flow into single conduits, fracture enlargement does continue with the product of maze caves. These results are consistent with the conclusions of Worthington et. al. (2000) that although the main portion of the flow in karstic aquifers is through the conduits, the main portion of the storage is in the fractures. The results are also consistent with the high well yields obtained from fractured dolomite aquifers.

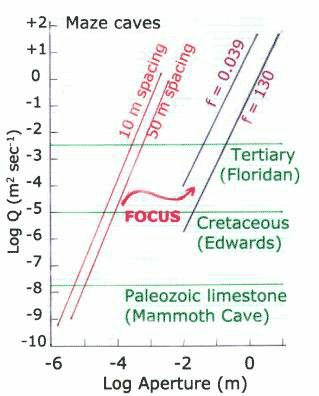
Fig. 2. Discharge through the components of the triple permeability system as a function of aperture. The horizontal lines are the matrix contribution. The lines labeled 10 m and 50 m spacing are the fracture contributions at the specified fracture spacing. The lines for the conduit contribution are labeled with the chosen values for the Darcy-Weisbach friction factors, f = 0.039 and f = 130.

Conduit systems do indeed dominate the flow system in many carbonate aquifers. However, in order for them to develop there must be focusing mechanisms to drain off water from the fractures before they develop wide apertures. Lowe?s (2000) inception horizon concept is of importance as one of the focusing mechanisms. Further, the hydraulic gradient must be sufficient to drive the competitive process that leads to single conduits. Low gradient aquifers are again associated with maze caves and a dominance of fracture flow.

References

• Atkinson, T.C. 1977. Diffuse flow and conduit flow in limestone terrain in the Mendip Hills, Somerset (Great Britain). Journal of Hydrology 35: 93-110.
• Atkinson, T.C., P.L. Smart and T.M.L. Wigley.` 1983. Climate and natural radon levels in Castleguard Cave, Columbia Icefields, Alberta, Canada. Arctic and Alpine Research 15: 487-502.
• Brush, D.J. and N.R. Thomson. 2003. Fluid flow in synthetic rough-walled fractures: Navier-Stokes, Stokes, and local cubic law simulations. Water Resources Research 39: 1085, doi:10.1029/2002WR001346.
• Budd, D.A. and H.L. Vacher. 2002. Facies control on matrix permeability in the upper Floridan Aquifer, west-central Florida: Implications for diffuse flow. Karst Waters Institute Special Publication 7, 14-24.
• Gale, S.J. 1984. The hydraulics of conduit flow in carbonate aquifers. Journal of Hydrology 70: 309-327.
• Jeannin, P.-Y. 2001. Modeling flow in phreatic and epiphreatic karst conduits in the Hölloch Cave (Muotatal, Switzerland). Water Resources Research 37: 191-200.
• Konzuk, J.S. and B.H. Kueper. 2004. Evaluation of cubic law based models describing single-phase flow through a rough-walled fracture. Water Resources Research 40: W02402, doi:10.1029/2003WR002356.
• Lauritzen, S.-E., J. Abbott, R. Arnesen, G. Crossley, D. Grepperud, A. Ive and S. Johnson. 1985. Morphology and hydraulics of an active phreatic conduit. Cave Science 12: 139-146.
• Lowe, D.J. 2000. Role of stratigraphic elements in speleogenesis: The speleoinception concept. In Speleogenesis: Evolution of Karst Aquifers, A. Klimchouk, D.C. Ford, A.N. Palmer and W. Dreybrodt, Eds., National Speleological Society, Huntsville, AL, USA, pp. 65-76.
• Scanlon, B.R., R.E. Mace, M.E. Barrett and B. Smith. 2003. Can we simulate groundwater flow in a karst system using equivalent porous media models? Case study, Barton Springs, Edwards Aquifer, USA. Journal of Hydrology 276: 137-158.
• White, W.B. 1999. Groundwater flow in karstic aquifers. Chap. 18 in The Handbook of Groundwater Engineering, J.W. Delleur, Ed., CRC Press, Boca Raton, FL, pp. 18-1 ? 18-36.
• White, W.B. 2002. Karst hydrology: recent developments and open questions. Engineering Geology 65: 85-105.
• Witherspoon, P.A., J.S.Y. Wang, K. Iwai, and J.E. Gale. 1980. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resources Research 16: 1016-1024.
• Worthington, S.R.H. 1991. Karst hydrogeology in the Canadian Rocky Mountains. Ph.D. thesis, McMaster University, Hamilton, Ontario, 380 pp.
• Worthington, S.R.H. 1999. A comprehensive strategy for understanding flow in carbonate aquifers. Karst Waters Institute Special Publication 5, 30-37.
• Worthington, S.R.H., D.C. Ford and G.J. Davies. 2000. Matrix, fracture and channel components of storage and flow in a Paleozoic limestone aquifer. In Groundwater Flow and Contaminant Transport in Carbonate Aquifers, I.D. Sasowsky and C.M. Wicks, Eds., A.A. Balkema, Rotterdam, pp. 113-128.
• Worthington, S.R.H., G.M. Schindel and E.C. Alexander, Jr. 2002. Techniques for investigating the extent of karstification in the Edwards Aquifer, Texas. Karst Waters Institute Special Publication 7, 173-175.