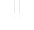Centre d'Hydrogéologie, University of Neuchâtel
11, rue Emile-Argand, CH-2000 Neuchâtel (Switzerland)
E-mail: This email address is being protected from spambots. You need JavaScript enabled to view it.
Abstract
One of the principal aims of hydrogeology is to propose a reasonably adequate reconstruction of the groundwater flow field, in space and in time, for a given aquifer. For example, interpretation of the chemical and isotopic composition of groundwater, understanding of the geothermal conditions (anomalies) or forecasting the possible effects of industrial waste disposals and of intensive exploitation nearly always would require the knowledge of the regional and/or local groundwater flow systems such as defined by Toth (1963). The problem of estimating the groundwater flow field in fractured and karstified aquifers is approached within the framework of a conceptual diagram showing the relationship between groundwater flow, hydraulic parameters (aquifer properties and boundary conditions), distribution of voids and geological factors.
Autoregulation between groundwater flow and karst aquifer properties, duality of karst, nested model of geological discontinuities, scale effect on hydraulic parameters and use of numerical finite element models to check the interpretation of the global response of karst springs are some of the subjects addressed by the author. Inferences on groundwater flow regime with respect to the stage of karst evolution can be made only if the hydraulic parameter fields and the boundary conditions are known by direct observations, or estimated by indirect methods for the different types of karst. Practical considerations on the monitoring strategies applied for karst aquifers, and on the interpretation of the global response obtained at karst springs will complete the paper, which throughout reflects the point of view of a hydrogeologist.
Keywords: karst hydrogeology, karst aquifers, numerical modelling of karst flow, spring hydrographs
1. Introductory remarks
1.2. Relation between groundwater flow field, hydraulic parameters and geological factors
In hydrogeology we do not study karstification or karst evolution for themselves: we are interested in them only in so far as they exert an influence on the groundwater flow field. The reconstruction of a regional groundwater flow field, which is consistent with a given hydraulic conductivity field and with given boundary conditions, nearly always requires the use of numerical models. Presently we have a wide variety of equations describing the groundwater movement in various domains (see, for example, for saturated/unsaturated flow and groundwater/surface-water interaction Tregarot 2000; Ababou et al. 1998) and we can solve them quite accurately by numerical models if we know, in the modelled region, the field of the relevant hydraulic parameters (hydraulic conductivity, storage coefficient, efficient porosity, etc., in each point of the aquifer), as well as the initial and the boundary conditions (mainly infiltration and fixed head values, such as altitude of springs, lakes or rivers).
With the use of numerical models explicitly appears a very important fact: as groundwater flow depends only on hydraulic parameters and on boundary conditions, the geological, geomorphological and climatic factors will exert their influence on the groundwater movement solely through the hydraulic parameter fields and the boundary conditions. If we could measure, for example, the value of the hydraulic parameters everywhere in the Earth's crust, we ought not to bother about fractures, faults, karst channels, lithologies and other geological factors: we could simulate and predict the behaviour of the groundwater flow systems without geology. In other words, if we will give a hydrogeological meaning to the geological, geomorphological or climatic factors, if we will examine their influence on the groundwater flow field, then we have to "translate" them (if possible, explicitly) into boundary conditions and hydraulic properties of the aquifer.
Evidently enough, geology will influence the hydraulic conductivity and porosity through the distribution of "voids": increase of density, opening and connectivity of the voids will increase the hydraulic conductivity and the porosity. If fracture or microfracture families show well defined, preferred orientation, the hydraulic conductivity may become anisotropic, thus conducting groundwater better in a direction than in another. At this stage sedimentation, diagenesis and tectonic deformations are the principal processes influencing the void distribution in sedimentary rocks.
Complications may appear in carbonate rocks, which are soluble in water: the groundwater in movement may dissolve the limestone around the existing voids, thus increasing their opening and the hydraulic conductivity of the aquifer. The amount of dissolved limestone, the enlargement of fractures depend obviously on the chemical composition of the rock and of the water, but the relative karstification of the various fracture families will depend mainly on the direction and the magnitude of the groundwater flux density vector ![]() given by Darcy's law, where
given by Darcy's law, where ![]() is the hydraulic conductivity tensor and
is the hydraulic conductivity tensor and ![]() is the hydraulic head (Bedinger 1966; Kiraly et al. 1971). Considering that
is the hydraulic head (Bedinger 1966; Kiraly et al. 1971). Considering that
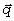 depends on the hydraulic conductivity and the hydraulic gradient,
depends on the hydraulic conductivity and the hydraulic gradient,- the hydraulic conductivity depends on the opening of pores and fractures,
- the opening of karstified pores and fractures is strongly influenced by the direction and magnitude of
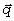 during the previous stages of the groundwater flow field,
during the previous stages of the groundwater flow field,
we arrive in a very important and characteristic feed-back loop of the karstification process. It shows, that in karst aquifers the hydraulic conductivity field and the void distribution result not only from the geological history of the rocks, but also from the whole history, from the whole evolution of the groundwater flow systems: the present state of the groundwater flow field and the hydraulic conductivity field is the result of successive, short-term and long-term autoregulations between the fields ![]() ,
, ![]() ,
, ![]() and the boundary conditions (infiltration, altitude of discharge areas, etc.). Indeed, we have to emphasize, that geographical position of the recharge and discharge areas represent boundary conditions for the flow field
and the boundary conditions (infiltration, altitude of discharge areas, etc.). Indeed, we have to emphasize, that geographical position of the recharge and discharge areas represent boundary conditions for the flow field ![]() and their evolution in time (paleo-geography, geomorphology) could influence karstification and hydraulic conductivity field as much as other geological factors (facies, structure, etc.).
and their evolution in time (paleo-geography, geomorphology) could influence karstification and hydraulic conductivity field as much as other geological factors (facies, structure, etc.).
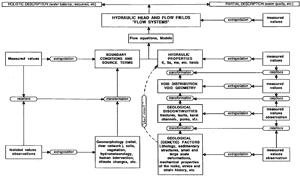
All these conceptual relations between groundwater flow systems, hydraulic parameters, void distribution and geological factors are represented as a partly self-regulating system in the diagram of Fig. 1. The feed-back of the flow field on the hydraulic conductivity field will produce it's effect only after a "certain time", thus giving an important role to the "duration", to the "history" in the karstification process. This means, that understanding the karstification in a given aquifer would require the knowledge of the "paleo-hydraulic" conditions, as it was proposed by Mandel (1966) and Kiraly et al. (1971).
Fig. 1. Schematic representation of the relations between groundwater flow field, hydraulic properties and geological factors in karst aquifers (after Kiraly 1975, modified).
1.1 Duality of karst aquifers
The partly self-regulating system of Fig. 1 is, in fact, a graphic representation of the karst development according to the ideas of Rhodes and Sinacori (1941), Swinnerton 1949, LeGrand and Stringfield 1966, Mandel 1966 and Bedinger 1966). They assume that dissolution starts in non-karstified fractured rocks where the heterogeneity of the permeability field is not very important (1 to 50?). Groundwater flow will enhance the dissolution particularly in fractures which are sub-parallel to the local hydraulic gradient and which are in the vicinity of the free groundwater table (Bedinger 1966). The heterogeneity of the hydraulic conductivity field increases (up to 1 to 1 million!) and the zones with higher permeability will represent discharge regions with respect to the lower permeability volumes.
The competition for the drainage between high-conductivity zones will lead to the capture of the slower developing branches and will contribute to the unification of the karst channel network and to the "concentration" of the discharge areas: the karst springs will be less in number but more important as far as the discharge is concerned. The hydrograph of the remaining springs becomes more and more "karstic", i.e. the reaction of the springs to input events will become more and more "violent", with rapidly increasing and rapidly decreasing peak-flow. This is a sign that infiltration becomes strongly heterogeneous, too, with an always growing part of concentrated infiltration. Thank to the works of (Burger 1956; Schoeller 1967; Berkaloff 1967; Forkasiewicz and Paloc 1967; Drogue 1967; Mangin 1975) we may consider the hydrograph of karst springs as one of the most important indirect indicators on the structure of the hydraulic conductivity field and on the heterogeneity of the infiltration in a karst aquifer.
In this "mature" karst aquifer we may speak of the "duality of karst" (Kiraly 1994). Indeed, the organized heterogeneity of the hydraulic conductivity field may be schematized by a high permeability, generally unknown channel network with kilometer wide "meshes", which is "immersed" in a low permeability fractured limestone volume, and is well connected to a local discharge area, the karst spring. The duality of karst aquifers is a direct consequence of this structure:
- duality of the infiltration processes ("diffuse" or slow infiltration into the low permeability volumes, "concentrated" or rapid infiltration into the channel network);
- duality of the groundwater flow field (low flow velocities in the fractured volumes, high flow velocities in the channel network);
- duality of the discharge conditions (diffuse seepage from the low permeability volumes, concentrated discharge from the channel network at the karst springs).
Note that besides the rivers disappearing in sinkholes, the concentrated infiltrations could be enhanced by the rapid drainage in a high conductivity "skin" at shallow depth: the epikarst (Mangin 1975).
The above presented karst development assumes a very simple and favorable hydrogeological setting, i.e. open or denuded karst. For more complicated hydrogeological settings the reader should consult the beautiful book edited by (Klimchouk et al. 2000), particularly the papers between pages 45 and 100. In the following of the present paper we will show the nested structure of the geological discontinuities, their relation to the hydraulic conductivity tensor and a few hydrogeological consequences of the duality of karst aquifers.
2. The nested structure of the geological discontinuities
2.1 Qualitative observations in the field
Geological discontinuities exist at all scales: intragranular cracks not longer than a few microns, microfractures of a few millimetres or centimetres, fractures (in the usual sense) of metric or decametric length, faults of a few hectometres, kilometres or tens of kilometres, big fault zones extending over several hundreds of kilometres, or cave systems with length of tens of kilometres. In sedimentary rocks the bedding planes (stratification) represent very persistent, closely spaced (from a few centimetres to a few meters) discontinuities of considerable lateral extent (several kilometres). Geologists have developed a rather complicated genetic terminology of their own to designate rock discontinuities, but this terminology will not be used here. Following the International Society of Rock Mechanics Suggested Methods for Quantitative Description of Discontinuities in Rock Masses (Barton, 1978), we use only the generic term discontinuity and the somewhat more specific term fracture, to designate discontinuities of metric or decametric length.

Fig. 2. Illustration of the nested model concept (after Feuille d'Avis de Neuchâtel)
In most cases the enumerated discontinuities are not randomly oriented, but form families, even if the orientation of a family may change from place to place. This is quite normal given the fact that the orientation of the discontinuities must somehow be related to the rather complicated, past or present, regional and local stress fields (Chinnery 1965; Gramberg 1965). If the lateral extent of the discontinuities is greater than their spacing, it seems reasonable to suppose that families with different orientations will form more or less connected networks of discontinuities, with "meshes" of different magnitudes (Jamier and Simeoni 1979; Rouleau 1985). As the networks of different magnitudes coexist in the real systems, the fractured and karstified medium should be characterized by its nested structure of discontinuities. Even if the nested structure concept is a qualitative mental picture only, it allows to ask some important questions when we are investigating flow and mass transport in fractured and karstic media:
- Which magnitudes of the discontinuities are of interest for the investigated phenomena and which may be neglected.
- Which magnitudes could be averaged and which not (is it possible to combine the "discrete fracture" approach with the continuum approach).
- How could we quantify the nested structure of the discontinuities (if required).
- How do the presently used quantitative methods respect the existence of nested structures in the real systems (in randomly generated fracture or karst channel networks, for example).
- And finally, the most important question: could the nested structure of the geological discontinuities determine a nested structure of the hydraulic conductivity field?
Many of these questions will remain unanswered here. In spite of this fact, they deserve attention from a heuristic point of view.
2.2 The scale effect in nested structures
There is an abundant scientific literature on scale effect in fractured media. The interested reader will find the more recent references in Bear et al. (1994) or in Lee and Farmer (1993). In most of these papers the scale effect is investigated by applying the percolation theory or the renormalization theory to a schematic representation of the fractured aquifers. As the above theories don't apply to nested structures, all the schematic discontinuities are of the same order of magnitude, even if there is a certain statistical distribution allowed about the mean fracture length, the mean fracture orientation and the mean fracture opening. The obtained scale effect is related to the clustering of the interconnected discontinuities in randomly generated networks.
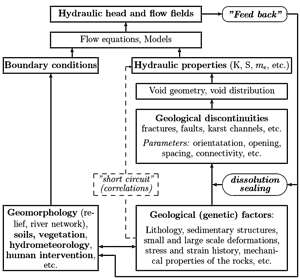
A different kind of scale effect could appear in the above described nested structures. The idea was developed for fractured and karstic limestone aquifers located in the Jura mountains (Switzerland) in the early seventies (Tripet 1972; Kiraly 1973, 1975), but the principle might well apply for non-carbonate aquifers, too. In these karstic aquifers, besides the common fracture network with "meshes" of a few meters, there must be a high-permeability channel network with wide, kilometric intervals, which is well connected to a discharge area, the karstic spring. Between the channels, the fractured rock mass has a low hydraulic conductivity, about ![]() to
to ![]() [m/s], values obtained by pumping tests in 300 to 400 m deep boreholes. Regional numerical models showed, that at a basin-wide scale the overall hydraulic conductivity must be 2000 to 5000 times higher than the "local" conductivity values measured in the boreholes (see Fig. 2). This important scale effect is due to the very high hydraulic conductivity of the widely spaced karst channel network. As most of the boreholes are located between the karst channels, the locally measured hydraulic conductivity values don't give any information on the existence of this scale effect. Basin-wide water balance studies and the use of regional numerical models are necessary to put forward the phenomenon.
[m/s], values obtained by pumping tests in 300 to 400 m deep boreholes. Regional numerical models showed, that at a basin-wide scale the overall hydraulic conductivity must be 2000 to 5000 times higher than the "local" conductivity values measured in the boreholes (see Fig. 2). This important scale effect is due to the very high hydraulic conductivity of the widely spaced karst channel network. As most of the boreholes are located between the karst channels, the locally measured hydraulic conductivity values don't give any information on the existence of this scale effect. Basin-wide water balance studies and the use of regional numerical models are necessary to put forward the phenomenon.
In non-carbonate fractured aquifers there is no karstic network. Nevertheless, it could happen that large discontinuities with a wide spacing have a higher hydraulic conductivity than closely spaced
Fig. 3. Scale effect on the hydraulic conductivity in fractured and karstified limestone aquifers (after Kiraly 1975, modified).
smaller ones, and in this case there will be a certain scale effect on the hydraulic conductivity: local values will not be the same as the overall regional values. This kind of scale effect is very different from what we obtain with the percolation or renormalization theory: it is the consequence of the nested structure of the hydraulic conductivity field inferred from the nested structure of the fractured and/or karstified medium.
The idea on the nested structure of the hydraulic conductivity suggests to go back to the real systems and check it. Instead of doing statistics on anonymous conductivity values, it would be far more interesting to obtain information about the spacing of the high-permeability zones, about the lateral extent of the high-permeability zones and about the connectivity of the high-permeability zones. Then it would be possible to compare the structure of the hydraulic conductivity field with the structure of the geological discontinuities. Because presently we are not yet able to answer such fundamental questions as how to predict actually water conducting zones from statistical information about geological discontinuities. Although based on qualitative observations and on inferences, the general ideas developed in these first pages will help to critically evaluate the techniques presented without many comments in the next sections.
2.3 Permeability tensor for fractures and intersections of fractures
The estimation of the hydraulic conductivity tensor from idealised fracture geometry was proposed by Romm and Pozinenko (1963). Snow (1969) presented a general method for individual fractures and Kiraly (1969) proposed to estimate the permeability tensor for both fractures and intersections of fractures. We have to emphasize that using the hydraulic conductivity tensor transforms the discontinuous real aquifer into an equivalent continuum.
Let us define N families of idealized fractures in the delta-neighbourhood of a point. The mean plane of the i-th family is characterized by ![]() = unit normal of the plane;
= unit normal of the plane; ![]() = average number of fractures in the direction of the normal;
= average number of fractures in the direction of the normal; ![]() = average aperture of the i-th family. In Darcy's law given by
= average aperture of the i-th family. In Darcy's law given by ![]() the hydraulic conductivity tensor
the hydraulic conductivity tensor ![]() may be calculated for the N families of fractures by
may be calculated for the N families of fractures by
![]() (1)
(1)
where ![]() = density of water;
= density of water; ![]() = acceleration due to gravity;
= acceleration due to gravity; ![]() = dynamic viscosity;
= dynamic viscosity; ![]() is the tensor product and I is the unit matrix. The geometric or intrinsic permeability
is the tensor product and I is the unit matrix. The geometric or intrinsic permeability ![]() is easily identified: it depends only on the fracture parameters
is easily identified: it depends only on the fracture parameters ![]() ,
, ![]() and
and ![]() .
.
Let us idealize the intersections of two families of fractures by a bundle of tubes, which is characterized by ![]() = unit vector parallel to the i-th bundle;
= unit vector parallel to the i-th bundle; ![]() = number of tubes per unit surface perpendicular to
= number of tubes per unit surface perpendicular to ![]() ;
; ![]() = average diameter of the tubes in the i-th bundle. Making use of the Hagen-Poiseuille formula we obtain the global hydraulic conductivity tensor for M bundles of intersections by
= average diameter of the tubes in the i-th bundle. Making use of the Hagen-Poiseuille formula we obtain the global hydraulic conductivity tensor for M bundles of intersections by
![]() (2)
(2)
Knowing the fracture parameters for N families of fractures allows to estimate the parameters for the M bundles of intersections:
![]() (number of bundles)
(number of bundles)
![]() (orientation of k-th bundle)
(orientation of k-th bundle)
![]() (density of intersections)
(density of intersections)
where ![]() is the vector product;
is the vector product; ![]() ;
; ![]() . Obviously, the most ticklish problem is to estimate
. Obviously, the most ticklish problem is to estimate ![]() when
when ![]() .
.
The idealized representation of the geological discontinuities, which allowed to estimate the permeability tensor, is never totally realized in the real systems. Real fractures are not evenly spaced, their aperture is not constant in the fracture plane, they are not strictly parallel to each other even in the same family, their lateral extent ("length") may vary, in a word: the fractured medium is not only anisotropic, but heterogeneous, too. If the ![]() -neighbourhood for which we estimate the permeability tensor is "big" with respect to the local heterogeneities, the [K] tensor will not correctly describe the behaviour of the real system. This simply indicates that one [K] tensor alone cannot describe a whole region and the
-neighbourhood for which we estimate the permeability tensor is "big" with respect to the local heterogeneities, the [K] tensor will not correctly describe the behaviour of the real system. This simply indicates that one [K] tensor alone cannot describe a whole region and the ![]() -neighbourhood has to be diminished. In this case the heterogeneities will appear clearly in the interior of the region. A last remark: the continuity of the fractures is required only in the
-neighbourhood has to be diminished. In this case the heterogeneities will appear clearly in the interior of the region. A last remark: the continuity of the fractures is required only in the ![]() -neighbourhood, not over the entire region.
-neighbourhood, not over the entire region.
2.4 The "serial type model" of the void geometry in fractured rocks
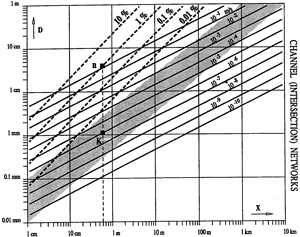
In three orthogonal and equally developed fracture families, or intersection bundles, the hydraulic conductivity is isotrope and its magnitude depends on the spacing ![]() (or
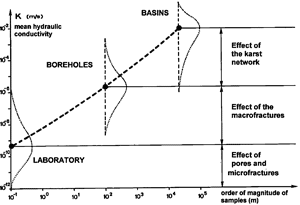
(or ![]() ) and the aperture d (or D). In a diagram log d versus log x (or, for the intersections: log D versus log X) constant permeabilities or constant porosities appear as straight lines (see the diagrams of Figs 3a and 3b). These diagrams allow to rapidly estimate the permeability value for more or less connected networks of discontinuities, with "meshes" of different magnitudes. The dark zones represent spacing and aperture values which seem reasonable in real fractured or karstic aquifers and show an important scale-effect on the hydraulic conductivities (but not, or less, on the efficient porosities) with progressive karstification.
) and the aperture d (or D). In a diagram log d versus log x (or, for the intersections: log D versus log X) constant permeabilities or constant porosities appear as straight lines (see the diagrams of Figs 3a and 3b). These diagrams allow to rapidly estimate the permeability value for more or less connected networks of discontinuities, with "meshes" of different magnitudes. The dark zones represent spacing and aperture values which seem reasonable in real fractured or karstic aquifers and show an important scale-effect on the hydraulic conductivities (but not, or less, on the efficient porosities) with progressive karstification.
Fig. 4. Hydraulic conductivity and efficient porosity values for various networks of fractures (left)
and intersections of fractures or karst channels (right).
In the Swiss Jura Mountains we have field measurements on the hydraulic conductivity (about ![]() m/s), on the efficient porosity (about 0.4 to 1%) and on the fracture spacing (about 0.6 m). If we represent these values on the diagrams of Fig. 3a and Fig. 3b (see points K and n), we cannot find a unique fracture aperture or channel diameter which could "explain" both the permeability value and the efficient porosity value. In other words, the void geometry which determines the permeability is not the same as the void geometry which determines the efficient porosity. The efficient porosity value requires large openings in the fracture planes (up to 1 mm aperture) but the permeability value shows that these large voids are not well interconnected.
m/s), on the efficient porosity (about 0.4 to 1%) and on the fracture spacing (about 0.6 m). If we represent these values on the diagrams of Fig. 3a and Fig. 3b (see points K and n), we cannot find a unique fracture aperture or channel diameter which could "explain" both the permeability value and the efficient porosity value. In other words, the void geometry which determines the permeability is not the same as the void geometry which determines the efficient porosity. The efficient porosity value requires large openings in the fracture planes (up to 1 mm aperture) but the permeability value shows that these large voids are not well interconnected.
Combining the "fracture model" with the "intersection model" may represent a solution to the problem: the permeability is determined by the intersections of fractures (required diameter: about 1 mm) and the efficient porosity is determined by the larger voids in the plane of the fractures (required aperture: about 1 mm). The large openings are well connected to the intersections where the groundwater flows, but are poorly connected to each other. The above described void geometry is schematically represented in Fig. 4, which is not more than the "serial type model" of Scheidegger (1963) adapted to the three-dimensional fractured medium (Kiraly 1994). The idea was taken up later by Hauns, Jeannin and Hermann (1998) who applied it to big karst channels by simulating the changes in width and in depth of the underground rivers. Interestingly enough, the "serial type model" of the void geometry could explain all particularities of the empirical break-through curves observed in fractured and karstic rocks (particularly the "tailing" of the break-through curves), without adsorption and desorption phenomena, and without molecular diffusion into the "immobile water". The above presented example shows that even theoretical and very schematic representations may be useful, provided they are confronted with the observations made in the real system.
3. Interpretation of karst spring hydrographs based on the global methods
3.1 The global response of karst aquifers
In the previous chapters we briefly presented the general nested structure of geological discontinuities and the duality of karst aquifers. How do their consequences manifest in the global response of real karst springs?
The behavior of the karst spring (hydrograph, water temperature, chemical or isotopic composition, etc.) represents the "global response" of the karst aquifer to input events. As the available data on the three-dimensional distribution of the hydraulic parameters are very limited, the more easily obtained global response is often used to make inferences (sometimes even contradictory inferences) on the infiltration and groundwater flow processes, as well as on the hydraulic parameter fields and the degree of karstification of the aquifer. In most cases, interpretations are based on the analysis of recession hydrographs by using different hydrograph separation methods (Burger 1956; Forkasiewicz and Paloc 1967; Drogue 1972; Mangin 1975; Bonacci 1987, 1993), statistical analysis of the whole spring hydrograph (Mangin 1984; Dreiss 1982; Labat 2000), or analysis of transfer functions between input (infiltration) and output (spring hydrograph) obtained by black-box or grey-box models. A short critical review of these methods is presented by (Eisenlohr et al. 1997) and a more detailed presentation is found in Jeannin and Sauter (1998). In this paper we will only propose a few critical remarks concerning some of the usual interpretations.
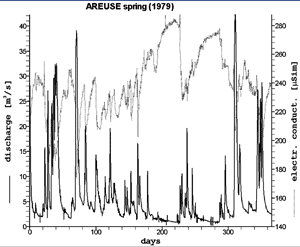
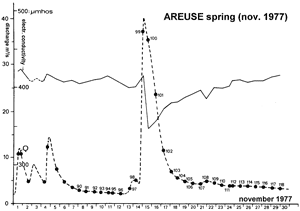
Fig. 6. represents the hydrograph of a typical karst spring, the Areuse spring in the Jura mountains (Switzerland) for 1979, as well as the registered electric conductivity curve giving an indirect indication on the mineralization of the spring water. The most striking features are the rapid variation of the spring discharge and the generally observed dilution effect of storm or snowmelt events on the spring-water chemistry. They suggest not only a well developed karstification of the aquifer, but also, that an important part of the infiltrations should be drained rapidly toward the high permeability karst channel network and the spring. Another important fact is the contrast between the rapidly decreasing recession curve after the peak
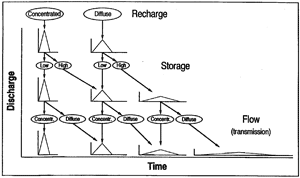
Fig. 7. Possible effects of the duality of recharge, storage and flow on the hydrograph of karst springs (from Hobbs and Smart 1986; in Jeannin and Sauter 1998).
flow, and the very slowly decreasing recession curve in the domain of feeble discharges. The interpretation seems intuitively evident: the two parts of the recession curve represent the rapid emptying of the high-permeability karst channels and the slow emptying of the low-permeability fractured volumes. All these observations seem more or less evident in the light of the duality of karst aquifers and we can guess, at least qualitatively, how the karst springs could react with increasing karstification. This is attempted in Fig. 7 proposed by Hobbs and Smart (1986) where the relations between input and output are represented very schematically as depending on the duality of infiltration, storage and groundwater flow.
3.2 Analysis of recession hydrographs
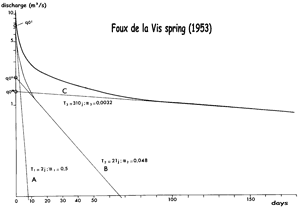
The recession curve is that part of the spring hydrograph which extends from a peak to the start of the next rise. The first aim of analysing the recession hydrograph was to estimate the volume of groundwater which could be drained by the karst spring in case of drought. As the last part of the slow recession curve can nearly always be approximated by an exponential, it is easy to integrate the approximated discharge from an arbitrary time ![]() till "infinity" and get a number for the groundwater volume which could flow out at the spring. The method says naturally nothing about the groundwater volume which is below the spring level, but all the same, it allowed a kind of quantitative comparisons between karst aquifers (Forkasiewicz and Paloc 1967) proposed that the total recession curve be represented as the sum of two, three or more exponential functions:
till "infinity" and get a number for the groundwater volume which could flow out at the spring. The method says naturally nothing about the groundwater volume which is below the spring level, but all the same, it allowed a kind of quantitative comparisons between karst aquifers (Forkasiewicz and Paloc 1967) proposed that the total recession curve be represented as the sum of two, three or more exponential functions:
![]()
where N is the number of exponentials, t is the time, ![]() are the discharges at t=0 and
are the discharges at t=0 and ![]() are the recession coefficients for each exponential (see Figs 8 and 9). In the interpretation, each exponential is thought to represent the depletion of a reservoir, the hydraulic conductivity of the reservoir being proportional to the recession coefficients
are the recession coefficients for each exponential (see Figs 8 and 9). In the interpretation, each exponential is thought to represent the depletion of a reservoir, the hydraulic conductivity of the reservoir being proportional to the recession coefficients ![]() .
.
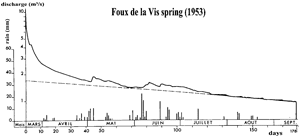
Fig. 8. Foux de la Vis spring (south of France): observed hydrograph during spring and summer of 1953.
The last part of the slow recession curve is approximated by an exponential (after Forkasiewicz and Paloc 1967)
Fig. 9. Illustration of the hydrograph separation method of (Forkasiewicz and Paloc 1967) as applied to the hydrograph
of Fig. 8.
Fig. 10. Separation of a theoretical hydrograph simulated by finite element model. There are only two classes of hydraulic conductivity in the model, yet the separation gives three exponentials (after Kiraly and Morel 1976b).
According to this interpretation, the exponential with the highest recession coefficient (![]() in Fig. 9) would represent the rapid depletion of the high permeability karst channels and the exponential with the lowest recession coefficient (
in Fig. 9) would represent the rapid depletion of the high permeability karst channels and the exponential with the lowest recession coefficient (![]() in Fig. 9) would correspond to the base-flow, i.e. to the slow depletion of the low hydraulic conductivity fracture network. Intermediate exponentials (see
in Fig. 9) would correspond to the base-flow, i.e. to the slow depletion of the low hydraulic conductivity fracture network. Intermediate exponentials (see ![]() in Fig. 9) are thought to represent the emptying of aquifer volumes with intermediate values of hydraulic conductivity. If the interpretation of the first and last exponential seems reasonable, the interpretation of the intermediate exponential is not necessarily true, as it was shown by (Kiraly and Morel 1976b). Fig. 10 shows the separation of a theoretical hydrograph simulated by an oversimplified 2-D finite element model. There are only two classes of hydraulic conductivity in the model, i.e. there is no aquifer volume with an intermediate hydraulic conductivity, the depletion of which causes the appearance of an intermediate exponential, yet the separation gives three exponentials. The intermediate exponential could simply be the result of transient phenomena in the vicinity of the high hydraulic conductivity channel network as we proposed it in Kiraly and Morel (1976b).
in Fig. 9) are thought to represent the emptying of aquifer volumes with intermediate values of hydraulic conductivity. If the interpretation of the first and last exponential seems reasonable, the interpretation of the intermediate exponential is not necessarily true, as it was shown by (Kiraly and Morel 1976b). Fig. 10 shows the separation of a theoretical hydrograph simulated by an oversimplified 2-D finite element model. There are only two classes of hydraulic conductivity in the model, i.e. there is no aquifer volume with an intermediate hydraulic conductivity, the depletion of which causes the appearance of an intermediate exponential, yet the separation gives three exponentials. The intermediate exponential could simply be the result of transient phenomena in the vicinity of the high hydraulic conductivity channel network as we proposed it in Kiraly and Morel (1976b).
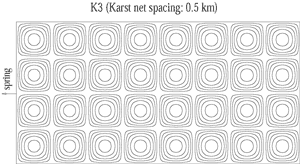
Fig. 11. Two nearly exponential recession hydrographs simulated by 2-D finite element models (see Fig. 12). The same geometry and the same hydraulic conductivities are used for the two models, only the channel network is more dense in model K3.
Fig. 12. Two finite element models with the same geometry and the same hydraulic conductivities, but with different channel network densities. Fig. 11 shows that depletion and "base-flow" are very different for the two "aquifers".
The models show that the last exponential represents the depletion of the low hydraulic conductivity fractured volumes, exactly as assumed in the generally accepted interpretation. It is, however, not true that the last recession coefficient ![]() of the base-flow depends on the hydraulic properties of the only low permeability volumes. In fact, it depends greatly on the geometry, the hydraulic conductivity and the density of the high permeability channel network. Fig. 11 shows two nearly exponential recession hydrographs simulated by 2-D finite element models (see Fig. 12). The same geometry and the same hydraulic conductivities are used for the two models, only the channel network is more dense in model K3. The recession coefficient is greater for K3, although the low permeabilities are the same for K1 and K3.
of the base-flow depends on the hydraulic properties of the only low permeability volumes. In fact, it depends greatly on the geometry, the hydraulic conductivity and the density of the high permeability channel network. Fig. 11 shows two nearly exponential recession hydrographs simulated by 2-D finite element models (see Fig. 12). The same geometry and the same hydraulic conductivities are used for the two models, only the channel network is more dense in model K3. The recession coefficient is greater for K3, although the low permeabilities are the same for K1 and K3.
It should be understood that the recession coefficient ![]() is a global parameter and will depend on the global configuration of the karst aquifers (even on their form and their extension). Using it to compute the hydraulic properties of the low permeability volumes could end up with very misleading conclusions.
is a global parameter and will depend on the global configuration of the karst aquifers (even on their form and their extension). Using it to compute the hydraulic properties of the low permeability volumes could end up with very misleading conclusions.
3.3 Critical remarks on the chemical or isotopic hydrograph separation methods
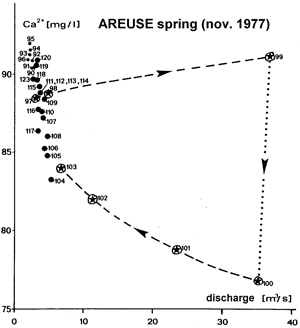
Fig. 6 showed the generally observed dilution effect of storm or snowmelt events on the spring-water chemistry. This suggests that an important part of the infiltrated "fresh-water" should be drained rapidly toward the high permeability karst channel network and the spring. Fig. 13 and 14 show the dilution phenomenon in detail in the case of a single peak flow of the Areuse spring. Careful sampling of the spring water before, during and after the peak flow allowed to visualize the variation of the calcium content, represented in Fig. 14. It shows that during the slow depletion of the low permeability volumes the karst channels are filled up with highly mineralised water characterizing the base-flow. Concentrated infiltration of fresh water determines the dilution effect during the peak flow, by mixing "old" water and "new" water in the karst channels. The "diluted" water is evacuated from the karst channels during the rapid recession and is progressively replaced by the "old" water of the base-flow (samples 100 to 104 in Fig. 14). These observations do not contradict the general ideas on the duality of karst and careful sampling (rising and falling limbs of peak hydrographs) and chemical analysis of spring water during input events appear as very important auxiliary methods for the understanding groundwater flow.
The idea of taking advantage of the quite general dilution effect by separating the whole hydrograph of a river or a karst spring into a "new-water" component and an "old-water" component was popularised in the mid 1970s and remained more or less widely used for the last 25 years (Martinec et al. 1974, 1979, 1982; Fritz et al. 1976; Dreiss 1989; Harum and Fank 1992; Gu 1992). The principle is simple, but many underlying hypotheses remain implicit, never clearly stated.
Let us define ![]() = spring discharge,
= spring discharge, ![]() = concentration of a "substance" in the spring water,
= concentration of a "substance" in the spring water, ![]() = old water component,
= old water component, ![]() = old water concentration,
= old water concentration, ![]() = new water component,
= new water component, ![]() = new water concentration. Most authors start from a very simplified mass balance:
= new water concentration. Most authors start from a very simplified mass balance:
![]() with
with ![]() (3)
(3)
expressing ![]() we have
we have ![]() with
with![]()
![]()
Fig. 13. Single discharge peak of the Areuse spring and dilution effect shown by the electric conductivity curve. Small black, numbered circles represent spring-water samples for chemical analysis (after Kiraly and Muller 1979).
Fig. 14. concentration versus discharge for the single peak shown in Fig. 13. Observe the dilution between samples 99 and 100 and the clustering of points located on the slow recession hydrograph (after Kiraly and Muller 1979).
This is a classical end member mixing analysis (EMMA) with ![]() and
and ![]() as end members. In most cases
as end members. In most cases ![]() is chosen to be the concentration of the base-flow and
is chosen to be the concentration of the base-flow and ![]() is the concentration of the storm or snowmelt water. When applied to real cases, the method gives nearly always a very important old water component: up to 60% or 70% of the peak flow. As long as the chemical or isotopic hydrograph separation is restricted to the "old water" and "new water" concept, there is nothing to say about these definitions.
is the concentration of the storm or snowmelt water. When applied to real cases, the method gives nearly always a very important old water component: up to 60% or 70% of the peak flow. As long as the chemical or isotopic hydrograph separation is restricted to the "old water" and "new water" concept, there is nothing to say about these definitions.
What should be however severely criticized, is the commonly accepted hydrologic and hydrogeologic interpretation of the components. As ![]() was taken to be the tracer concentration of the base-flow (Martinec et al. 1974, 1979, 1982; Fritz et al. 1976) and many others do not hesitate to equate the old water component
was taken to be the tracer concentration of the base-flow (Martinec et al. 1974, 1979, 1982; Fritz et al. 1976) and many others do not hesitate to equate the old water component ![]() with the hydrodynamic base-flow
with the hydrodynamic base-flow ![]() , i.e. with the groundwater discharge into the rivers or with the discharge of the low-permeability fractured volumes into the karstic network. The old water component is then compared (and opposed) to the "conventional" base-flow estimate, generally obtained by the backward extrapolation of an exponential recession curve (see, for example, Fig. 9).
, i.e. with the groundwater discharge into the rivers or with the discharge of the low-permeability fractured volumes into the karstic network. The old water component is then compared (and opposed) to the "conventional" base-flow estimate, generally obtained by the backward extrapolation of an exponential recession curve (see, for example, Fig. 9).
The comparison nearly always shows a high proportion of "old water" in the river or karst spring discharge even during flood events: ![]() may be as important as 60% or 70% of the total discharge
may be as important as 60% or 70% of the total discharge ![]() during peak flow, much more than the "conventional" base-flow estimate. Equating
during peak flow, much more than the "conventional" base-flow estimate. Equating ![]() with the base-flow
with the base-flow ![]() leads many authors to accept a much higher infiltration rate into the aquifers or into the low-permeability (!!) fractured volumes than the "conventional" estimates, the infiltrations being supposed to increase the hydraulic gradients and to force the older groundwater to rapidly discharge into the rivers or into the high-permeability karstic channels (see, for example, Martinec et al. 1982). Unfortunately the authors do not produce any empirical gradient and permeability measurements which would allow, together with the drainage length, for the hydraulic proof of the above mentioned interpretation. As a matter of fact it can be shown very easily, even with an oversimplified double reservoir model, that old water component and base-flow are two concepts totally different.
leads many authors to accept a much higher infiltration rate into the aquifers or into the low-permeability (!!) fractured volumes than the "conventional" estimates, the infiltrations being supposed to increase the hydraulic gradients and to force the older groundwater to rapidly discharge into the rivers or into the high-permeability karstic channels (see, for example, Martinec et al. 1982). Unfortunately the authors do not produce any empirical gradient and permeability measurements which would allow, together with the drainage length, for the hydraulic proof of the above mentioned interpretation. As a matter of fact it can be shown very easily, even with an oversimplified double reservoir model, that old water component and base-flow are two concepts totally different.
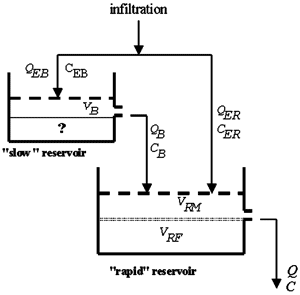
Let us represent a karst aquifer by the simplified two-reservoir model of Fig. 15. The slow reservoir simulates the low permeability fractured volumes and the rapid reservoir represents the karst channels. The variables are defined as follows:
![]() = infiltration into slow reservoir;
= infiltration into slow reservoir; ![]() = concentration in
= concentration in ![]() , but it will not be used for the slow reservoir;
, but it will not be used for the slow reservoir; ![]() = ground-water volume in the slow reservoir;
= ground-water volume in the slow reservoir; ![]() = base-flow;
= base-flow; ![]() = concentration of the base-flow;
= concentration of the base-flow; ![]() = direct infiltration into the karst channels;
= direct infiltration into the karst channels; ![]() = concentration of the direct infiltration;
= concentration of the direct infiltration; ![]() = volume of groundwater which is located above the spring level (it can flow out);
= volume of groundwater which is located above the spring level (it can flow out); ![]() = volume of groundwater below the spring level (the volume is fixed);
= volume of groundwater below the spring level (the volume is fixed); ![]() = discharge of the spring;
= discharge of the spring; ![]() = concentration of the spring-water. It appears clearly that
= concentration of the spring-water. It appears clearly that ![]() is
is ![]() and
and ![]() is
is ![]() . Due to the important residence time of the groundwater in the slow reservoir it is assumed that
. Due to the important residence time of the groundwater in the slow reservoir it is assumed that ![]() is more or less constant. We assume, in addition, an exponential depletion (emptying) for each reservoir and in this case the recession coefficient
is more or less constant. We assume, in addition, an exponential depletion (emptying) for each reservoir and in this case the recession coefficient ![]() is the ratio between the discharge and the volume of the reservoir:
is the ratio between the discharge and the volume of the reservoir: ![]() =
=![]() /
/![]() and we can pass from
and we can pass from ![]() to
to ![]() or from
or from ![]() to
to ![]() easily. Two differential equations will describe the "flow problem":
easily. Two differential equations will describe the "flow problem":
![]() (4)
(4)
![]() (5)
(5)
A third differential equation will describe the mass balance for the "tracer", where the total mass of tracer in the rapid reservoir is ![]() :
:
![]() or
or
![]()
![]() (6)
(6)
Equation 6 will reduced to the dashed box, i.e. to equation 3, if the first two terms are zero. But this would imply that there is no water in the karst channels (![]() is zero!), and/or the concentration in the spring water is constant. These are unrealistic conditions, thus equation 3 cannot be used to calculate, even approximately, the base-flow .
is zero!), and/or the concentration in the spring water is constant. These are unrealistic conditions, thus equation 3 cannot be used to calculate, even approximately, the base-flow .
Replacing ![]() and rearranging the terms we obtain
and rearranging the terms we obtain
![]() (7)
(7)
Fig. 15. Simplified double reservoir model for karst aquifers
Equations 4, 5 and 7 are three simultaneous differential equations which can be solved by the Runge-Kutta method for ![]() ,
, ![]() and
and ![]() if we give
if we give ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() . It must be emphasized that in this simplified model the groundwater volume below the spring level,
. It must be emphasized that in this simplified model the groundwater volume below the spring level, ![]() , does not influence the spring discharge, but it will greatly influence the variation of
, does not influence the spring discharge, but it will greatly influence the variation of ![]() , i.e. the dilution effect. For the same base-flow hydrograph or spring hydrograph, for example, very different dilution effects, thus very different "old water" components, could be obtained depending on the volume of
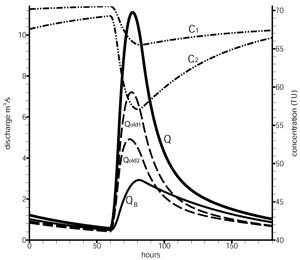
, i.e. the dilution effect. For the same base-flow hydrograph or spring hydrograph, for example, very different dilution effects, thus very different "old water" components, could be obtained depending on the volume of ![]() . This is the case illustrated in Fig. 16
. This is the case illustrated in Fig. 16
Fig. 16. Two dilution effects simulated by the double reservoir model of Fig. 15: only the fixed volume ![]() is changed from one variant to another. Observe that base-flow
is changed from one variant to another. Observe that base-flow ![]() and old water components
and old water components ![]() are not the same. The concentration is measured in Tritium Units.
are not the same. The concentration is measured in Tritium Units.
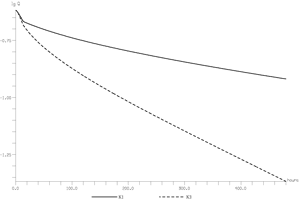
The example represented in Fig. 16 aimed to show that the old water component obtained by the usual chemical or isotopic hydrograph separation methods has not much to do with the hydrodynamic base-flow and in its present form rather leads to invalid inferences regarding the groundwater flow processes. In the double reservoir model the ratio between the recession coefficients of the slow reservoir and the rapid reservoir is about 1 to 10, and 50% of the infiltration is "diffuse", into the slow reservoir, and 50% is "concentrated", into the rapid reservoir. Both infiltration functions are triangular: 4 hours for the rising limb and 18 hours for the falling limb. The "tracer" is tritium: the concentration is 80 TU for the old water and 40 TU for the new or storm water. An important parameter for the dilution is ![]() , the volume of water in the karst channels located below the spring level. It is probably the principal responsible for the high old water content obtained by the chemical and isotopic hydrograph separation methods and the misinterpretation of the results. The ratio between the volumes
, the volume of water in the karst channels located below the spring level. It is probably the principal responsible for the high old water content obtained by the chemical and isotopic hydrograph separation methods and the misinterpretation of the results. The ratio between the volumes ![]() used for the two variants was 1 to 4. Increasing the fixed volume diminishes the dilution and increases the old water component (see the C1, C2 curves and the dashed old water curves Cold1, Cold2 in Fig. 16), while the base-flow does not change at all.
used for the two variants was 1 to 4. Increasing the fixed volume diminishes the dilution and increases the old water component (see the C1, C2 curves and the dashed old water curves Cold1, Cold2 in Fig. 16), while the base-flow does not change at all.
In spite of the many critical remarks presented above, we hope that this important dilution effect could be used, perhaps in the framework of a different paradigm, for a better understanding of karst and karstification. It deserves a better destiny than the only separation into a somewhat arbitrary new water and old water component.
4. Introduction to modeling karst aquifers
4.1. Aims of the modeling
Analysing the global response of karst springs stimulates our imagination and incites to make hypotheses about the structure of the aquifer, about the hydraulic parameter fields, about the groundwater flow processes, often about karstification and sometimes about the evolution of karst in the interior of the aquifer. The direct verification of the consequences of our hypotheses by field measurements in the interior of the karstic medium is, obviously, very difficult, if not impossible. The so called "global models", such as the double reservoir model used in the previous chapter, do not help much either, because we have no information on the spatial distribution of the variables and the parameters.
An indirect method of verification would consist in introducing the inferred karstic structures into a deterministic numerical model and then simulate the supposed processes and their effect on the "global response" of the aquifer (for example, the spring hydrograph), on the groundwater flow field, on the hydraulic head distribution, etc. The simulated behavior of the theoretical aquifer could then be compared to the usually accepted ideas on the groundwater flow processes in karst aquifers. This is the way followed by the research team of CHYN (Centre d'Hydrogéologie de l'Université de Neuchâtel) for years.
The aim of this chapter is to present the effect of the karst channel network and the epikarst zone on groundwater flow processes, as obtained by numerical finite element models simulating a few "theoretical" and oversimplified karst aquifers. The results, although "theoretical", have important practical consequences on the monitoring strategies applied for karst aquifers, on the interpretation of the global responses obtained at karst springs and on the estimation of the recharge of the low conductivity "capacitive" volumes. They suggest to ask such fundamental questions as: what is the meaning of "groundwater level" observations in boreholes when separated from hydraulic conductivity measurements; what is the meaning of the "groundwater table" represented by isolines (equipotentials) in karst aquifers; what is the hydraulic meaning of the "components" obtained by chemical or isotopic hydrograph separation methods; etc.
4.2. Model and reality
The reconstruction of a regional groundwater flow field, which is consistent with a given hydraulic conductivity field and with given boundary conditions, nearly always requires the use of numerical models. A model is not the reality, it is only the realization of a schematic and symbolic representation of the real system. The relations between "real system", "abstract scheme" and "numerical model" are represented in Fig. 17, which also shows the principal problems in modeling groundwater flow.
Starting from incomplete information on the aquifer to be modeled, a schematic representation of the real systemhas to be worked out first. Generally, the flow of the groundwater is represented by differential equations, which may change depending on the type of problem to solve (saturated-unsaturated flow, constant or variable density flow, multiphase flow, etc.). The flow equations contain a few parameters depending on the aquifer properties
Fig. 17. Principal problems in modeling groundwater flow. Observe that experimental methods should be used to check if the real system may be actually considered as a realization of the schematic representation (after Kiraly 1994, modified).
(hydraulic conductivity, specific storativity, effective porosity, etc.) and the real medium will be represented by the field of these parameters, i.e. by giving a parameter value to each point of the modeled region, even there where we have never made any observation. As the available data on the hydraulic parameters are very limited, it appears clearly that indirect estimation of the parameters and interpolation or extrapolation of the measured values will be unavoidable when modeling real aquifers (see Fig. 18). It must be emphasized that fractured and karstified media may present additional difficulties due to the strong local heterogeneity of the parameter fields. The karst channel network existing in the real system, for example, is never entirely known. Finally, the imposed and initial conditions complete the schematic representation, sometimes also termed the "conceptual model".
The second problem is related to the realization of a computer codebased on numerical methods which allow to solve the equations defined in the abstract scheme. The problem is far from being simple and in most cases the numerical model is only a more or less imperfect realization of the abstract scheme.
The third, very important problem in modelling groundwater flow is the transfer of the simulated results onto the real system. Strictly speaking, the simulated results are not "valid" but in the highly simplified scheme or numerical model, and their meaningful transfer onto the real system requires that simplifying assumptions and uncertainties on the data explicitly do appear as uncertainties on the results. This could help to avoid such ridiculous situations as trying to simulate observed piezometric heads to within a few centimetres, even though the schematised hydraulic conductivity field "ignores" the strong local heterogeneities existing in the real system.
As a matter of fact, schematic representation of the real system, numerical modeling and experimental field work should go hand in hand. The numerical models might be used from the very moment where the first hypotheses on geometry, hydraulic parameters and boundary conditions are explicitly formulated. Whatever may be the value of these hypotheses, the numerical model will give a "response", which represents the verifiable consequences of our inevitably hypothetical and schematic representation of the real system. Ultimately, it is the observed behaviour of the aquifer which will decide if our hypotheses are acceptable or not.
Fig. 18. Problems related to the reconstruction of hydraulic parameter and flow fields (after Kiraly 1975, modified)
Finally it must be emphasized that modeling is not just curve-fitting. As it was pointed out by Klemes (1986): "For a good mathematical model it is not enough to work well. It must work well for the right reasons. It must reflect, even if only in simplified form, the essential features of the physical prototype." This is particularly recommended in modeling karst aquifers.
4.3. Combined discrete channel and continuum approach by using finite element models
The nested model concept of the geological discontinuities was presented in the previous chapters. The modelling of this kind of nested structures nearly always requires the combination of the continuum approach with the discrete fracture or discrete channel model. At a regional scale, for example, the discrete fracture (or channel) model alone could not be realized at all, because of the tremendous amount of discontinuities (of different orders of magnitude) which ought to be introduced into the model.
On the other hand, the equivalent continuum approach alone would not show the effect of the regional fault zones or the regionally developed karst networks on the groundwater flow systems. So it seems reasonable to model the regional faults or karst networks by 2-D or 1-D "discrete" zones, whereas the volumes between them (which contain only lower order fractures or channels) might be modelled by a 3-D equivalent continuum. As a matter of fact, every discontinuity, which is "big" with respect to the size of the modelled region, should be represented by a discrete zone.
Numerical models using the finite element method are excellent for the combined discrete channel (or discrete fracture) and continuum approach, particularly if they allow for the combination of 1-D, 2-D and 3-D finite elements, as it was proposed by Kiraly (1979, 1985, 1988, 1994) and Helmig (1993). In this case, the high conductivity karst channel network is simulated by 1-D linear or quadratic finite elements, which are "immersed" between 2-D or 3-D linear or quadratic elements representing the low conductivity fractured limestone volumes.
The simulations presented in this paper were carried out by the computer codes FEN1 and FEN2. They have been developed at the Centre d'Hydrogéologie de Neuchâtel and simulate steady-state and transient, one-, two- or three-dimensional saturated groundwater flow by the finite element method. The computer programs allow for the incorporation of one-, two- or three-dimensional linear or quadratic elements within a three-dimensional network. The saturated, constant density, transient groundwater flow is represented by equation (8) where
![]() (8)
(8)
Ss is the specific storage coefficient, [K] is the hydraulic conductivity tensor, h is the hydraulic head and Q represents the general source/sink terms (infiltration, well discharges, etc.).
The formulation for the finite elements is based on the Galerkin weighted residual approach and the resulting system of linear equations is solved by the frontal elimination technique of Irons (1970). The time dependent problem is solved in FEN2 by using the robust Crank-Nicholson implicit time-stepping scheme. UFEN1 is a code derived from FEN1 and simulates saturated/unsaturated steady-state groundwater flow. In this paper it is used to simulate the free groundwater table in a theoretical "shallow" karst aquifer.
The computer codes allow the modeller to "concatenate" several aquifers into one model and this facility is used to link the epikarst with the mean aquifer. A slightly modified version of FEN2 offers another facility when used to simulate karst aquifers. By giving the identification number of the nodal points located on the karst channels, the program calculates the contribution of each 3-D element (i.e. low conductivity fractured volume) to the karst net. The sum of these contributions is simply the base-flow which can be compared to the total spring hydrograph.
Using the linear Darcy's law to simulate the groundwater flow in saturated karst channels represents only a crude approximation of the real system, but our aim was to obtain a rapid and rather "qualitative" indication on the effect of the enormous contrast between the hydraulic conductivities of fractured limestones (10-6 m/s) and karst channels (10 m/s or more). The conclusions presented in this paper will not be changed qualitatively with the simulation of turbulent flow: the effects due to concentrated infiltration into the channel network (inversion of gradients, negative base-flow, etc.), for example, will be only increased.
5. Presentation and discussion of a few results
5.1. The 2-D approach: some early results
In the 1970s it was possible to introduce 1-D elements between 2-D finite elements, and thus simulate the karst channel network in 2-D karst aquifers (Kiraly and Morel 1976a, 1976b). These early and very simplified 2-D karst models delivered quite interesting results.
- The simulation of the typical hydrograph of the karst springs (see Fig. 6), with the non-exponential rapid recession and the exponential slow recession, nearly always requires the introduction of a high permeability karst channel network in an otherwise low permeability aquifer volume.
- The duality of the hydraulic conductivity field causes an important scale effect in the model: nearly the whole aquifer volume has a very low hydraulic conductivity, however the global structure behaves as a highly transmissive system. Qualitatively it is the right type of structure: we are not very far from karst! We get even closer to karst with the infiltration problem.
- If the chosen spacing of the karst channels allows to simulate correctly the exponential part of the recession curve of springs, the correct simulation of the peak-flow and the rapidly decreasing non-exponential part of the recession curve requires, however, that more than 50% of the infiltration arrive in "concentrated" form, directly into the high conductivity channels. The concentrated infiltration in the model must have a physical counterpart in the real system. A sound hypothesis would be to suppose, that besides small rivers disappearing in sinkholes, an important part of the infiltration is drained rapidly, probably already at shallow depth in a thin high conductivity layer, towards the karst channel network and the karst spring. This would be the epikarst zone of Mangin (1975).
- The important concentrated infiltration, i.e. the duality of infiltration, has a very important consequence: the temporary inversion of the hydraulic gradients between the channels and the low permeability volumes.
- The temporary inversion of hydraulic gradients has an even more important consequence: the temporary reduction of the base-flow to zero in the vicinity of the peak-flow. And this is not good news for those who equate the old water component of a karst spring with the base-flow.
- At least, we have to mention that the recession coefficient of the last, exponential part of the depletion curve depends as much (if not more) on the conductivity and the density of the karst channels than on the hydraulic properties of the low permeability volumes.
Although very simple, these 2-D models were very good from a heuristic point of view. Even if in a very simplified and naive form, they had the most important properties of a karst aquifer (duality of the hydraulic conductivity field, duality of the infiltra-tion processes, duality of the groundwater flow field, concentrated discharge at the karst spring). The problems we met with them were actually relevant to the study of karst aquifers and suggested further investigations on the theoretical level, as well as in the domain of empirical field works.
5.2. The 3-D approach: the Epikarst model
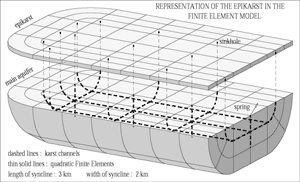
Earlier numerical experiments with 2-D Finite Element models showed the necessity to impose a high proportion of concentrated infiltrations in order to generate the typical "karstic" storm hydrographs (Kiraly and Morel 1976a, 1976b). It was supposed, that besides the rivers disappearing in sinkholes, the concentrated infiltrations would result from the rapid drainage in a high permeability "skin" at shallow depth: the epikarst (Mangin 1975). However, the epikarst layer could not be explicitly included in these 2-D models. To indirectly show its role, we explicitly introduced the epikarst layer in a "synthetic" 3-D Finite Element model and varied the proportion of the diffuse infiltrations with respect to the concentrated infiltrations resulting from the rapid drainage in the epikarst zone. As the model is transparent for the modeller, the simulated behaviour of the theoretical karst aquifer will clearly show the effect of epikarst not only on the spring hydrograph, but also on the baseflow component of the spring discharge, on the variation of hydraulic heads and fluxes during recharge and recession periods, as well as on the recharge conditions of the low permeability fractured volumes. The detailed results are presented in (Kiraly et al. 1995), we show here only a few diagrams without many comments.
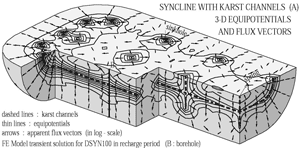
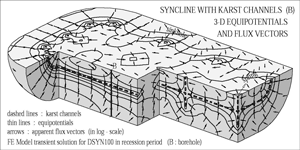
The diagram of Fig. 19a shows the 3-D geometry of a theoretical "half-syncline" drained by a very simplified high-permeability karst channel network. The karst channels are simulated by quadratic 1-D elements introduced "in sandwich" between the quadratic 3-D elements simulating the low-permeability fractured volumes. The epikarst is simulated by a 2-D finite element layer which will discharge into the channel network of the 3-D syncline, such as represented in Fig. 19a. The hydraulic heads are imposed at the base of the epikarst model (where the channels intersect the 2-D layer), and the calculated discharges are injected at each time-step into the channel network of the 3-D model. This will represent the concentrated infiltration function for the mean aquifer. Note that nearly the entire volume of the mean aquifer (including the high permeability channel network) is below the karst spring level, in the saturated zone.
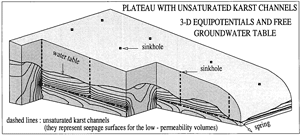
Fig. 19b represents a small "shallow" karst aquifer with an important vertical exageration. The aquifers of this type generally develop on plateaus or gently dipping cuestas. In the theoretical aquifer represented in Fig. 19b, the karst network is located above the spring level and is everywhere unsaturated. The channels are actually underground rivers and represent seepage surfaces with variable boundary conditions for the low-permeability fractured volumes. The free groundwater table was obtained by simulating the steady-state, saturated/unsaturated flow in the low-permeability volumes.
The karst syncline described above and the shallow karst of Fig. 19b represent two extremes and their reaction to important concentrated infiltrations will not be the same. The aim of including the "shallow karst" configuration in this paper is to remind the reader of the diversity of karst aquifers and to avoid abusive generalizations of the results obtained by the saturated karst syncline model.
The hydraulic parameters are the same for all variants of the epikarst model. The hydraulic conductivities K are realistic: 5 * 10-6 [m/s] for the low-permeability fractured volumes and 100 [m/s] for the high-permeability karst channels. In the 2-D epikarst layer the transmissivity T is relatively high: about 5 * 10-2 m2/s. Linear Darcy's law is used throughout the models.
Fig. 19b. Shallow karst aquifer model, with unsaturated karst channels.
The specific storage coefficients Ss are kept artificially low in order to "accelerate" the evolution of the simulated hydraulic head and flow field. In the channel network the values of Ss are 400 to 500 times higher than in the low-permeability fractured volumes.
Finally it must be emphasized that we use in the model a very simplified karst channel network. In real systems the karst network is hierarchically organized, with lower and higher order branches having lower and higher hydraulic conductivity values. In the above described model all branches of the karst network are of the same order of magnitude and have the same hydraulic conductivity.
The volume of the total infiltrations remains the same in each variant, but the proportion of the diffuse and concentrated infiltrations will change from one variant to another. Four cases have been simulated:
- DSYN0: 100% diffuse infiltration
0% drained by the epikarst - DSYN20: 80% diffuse infiltration
20% drained by the epikarst - DSYN50: 50% diffuse infiltration
50% drained by the epikarst - DSYN100: 0% diffuse infiltration
100% drained by the epikarst
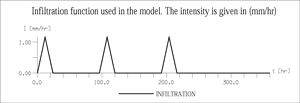
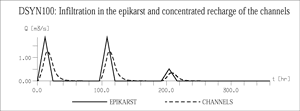
Fig. 20. Intensity of infiltration (above), as well as total recharge function of the epikarst and concentrated recharge function of the karst channels (below) for variant DSYN100
Fig. 20 represents the intensity of infiltration, as well as the total recharge function of the epikarst and the concentrated recharge function of the karst channels for variant DSYN100. There are three input events ("storms"), of duration of 24 hours each. During the first and second event the infiltrations are distributed over the whole syncline. During the third "storm", infiltration takes place only on a small stripe in the middle part of the model, representing about 30% of the total infiltration area.
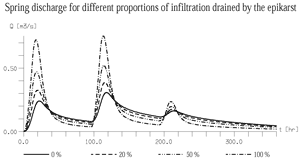
5.3. Effect on the shape of the spring hydrograph and on the hydraulic heads
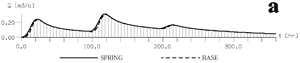
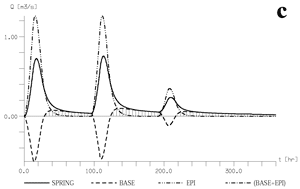
Fig. 21 is self-explanatory: it represents the spring hydrographs for different proportions of infiltration drained by the epikarst into the high-permeability channel network. It appears clearly that without some kind of concentrated infiltrations we cannot simulate the typical karstic reactions of the spring. The rise of the groundwater table in the low-permeability volumes cannot "press" enough water into the karst channels to cause a typical karstic storm hydrograph at the spring. It seems reasonable to admit that in most "open" karst aquifers more than 40% of the infiltrations should be drained rapidly into the karst channels (also see Kiraly and Morel 1976a).
The high proportion of "old water" component obtained by the method EMMA (End Member Mixing Analysis) does not represent a serious argument against important concentrated infiltrations into the channel network, because the method is not related to any consistent groundwater flow model. Indeed, in the period preceding the storm event an important quantity of "old water" may be stored not only in the epikarst zone and in the unsaturated zone, but also in the high-permeability karst network itself, at least in the channels located below the spring level. This "old water" flows out rapidly during the peak discharge, even if the low-permeability fractured volumes do not contribute to the peak-flow at all.
Fig. 21. Simulated spring hydrographs for different proportions of infiltration drained by the epikarst.
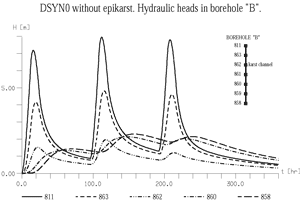
Fig. 22a. Variation of the hydraulic head
in borehole "B" for DSYN0.
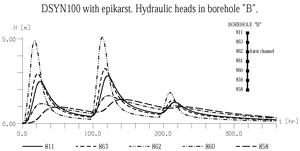
Fig. 22b.Variation of the hydraulic head in borehole "B" for DSYN100
Earlier numerical experiments with 2-D finite element models suggested that concentrated infiltrations might cause an inversion of the gradients between karst channels and low-permeability volumes (Kiraly and Morel 1976a, 1976b). These 2-D models cannot show, however, the vertical distribution of the hydraulic heads in a borehole. Taking advantage of the 3-D model, we "registered" the simulated heads in an imaginary borehole "B", the location of which is presented in Fig. 23a and 23b. The borehole intersects a karst channel and the hydraulic heads are measured at 7 points between the top and the base of the aquifer.
The results are represented for variants DSYN0 (no concentrated infiltrations, see Fig. 22a) and DSYN100 (100% of the infiltrations are concentrated, see Fig. 22b). Again, the figures are self-explanatory and need not many comments.
Fig. 23a. Hydraulic head field for DSYN100 in recharge period.
Fig. 23b. Hydraulic head field for DSYN100 in recharge period. Location of borehole "B" shown on the figures.
During the recharge period there is nearly always an inversion of gradients between the karst channel and the low-permeability volumes located below the channel. The concentrated infiltrations must be really important to produce the same inversion with respect to the low-permeability volumes located above the channel. The bloc-diagrams of Fig. 23a and 23b clearly show the recharge and drainage mechanism with epikarst and concentrated infiltration.
The practical consequences of these theoretical results are important: the hydraulic heads should be measured separately in the high-permeability segments and in the low-permeability segments of boreholes or piezometers. If we measure only one "groundwater level" in an otherwise heterogeneous borehole, the results will be rather misleading than helpful. Other practical consequences are related to the determination of the baseflow component, to the recharge mechanism of the low permeability fractured volumes, to the interpretation of the chemical or isotopic composition of the spring-water, etc.
5.4. Effect of the epikarst on the "base-flow" component of karst springs
In spite of the fact that the inversion of gradients between karst channels and low-permeability volumes is well known by many karst hydrogeologists, most of the graphically obtained base-flow hydrographs don't show the logical consequence, namely the zero (or negative) base-flow value during recharge periods. One of the few exceptions is found in (Tripet 1972), who suppressed the base-flow component of the Areuse spring during the recharge periods.
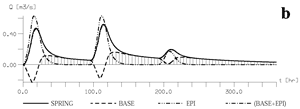
Taking advantage of the possibility to calculate the contribution of the low-permeability 3-D elements to the nodes located on the 1-D karst channels, we computed the baseflow component for each variant. The dramatic effect of the concentrated infiltrations on the base-flow component is presented in Fig. 24 for variants DSYN0, DSYN50 and DSYN100. The appearance of negative base-flow during the recharge period indicates that the karst channels inject more water into the low-permeability volumes than they drain. The volume of this recharge might not be very important, but the fact that the low-permeability volumes may be recharged "from the interior" should not be overlooked.
Another consequence of the negative baseflow appears when estimating the "rapid infiltration" from the spring hydrograph. Generally this is done by substracting the graphically determined baseflow component from the total discharge curve. Now, when the baseflow is negative, it should be added to the spring discharge, otherwise the intensity of the rapid or direct infiltration will be systematically underestimated (see Fig. 24b, 24c).
Fig. 24. Springflow, baseflow, epiflow and (epiflow+baseflow) for variants DSYN0 (a), DSYN50 (b) and DSYN100 (c). Note that concentrated infiltration (epiflow) may be greater, or even much greater than the spring discharge. The curve (baseflow+epiflow) is not visible, because it coincides almost exactly with the springflow.
As the model allows for the independent estimation of the baseflow and of the rapid or concentrated infiltration into the karst channel network (which will be called "epiflow", for short, in the following), we can take a critical look at the usually accepted chemical or isotopic hydrograph separation methods.
Fig. 24b, 24c show, that the "new water component" obtained by the End Member Mixing Analysis (EMMA) could not be identified with the "rapid recharge to the conduit system after a storm", as it was stated by Dreiss (1989, page 121). Indeed, the "new water component" obtained by EMMA must be always smaller than the spring discharge, but figures 24b and 24c indicate clearly that the rapid recharge into the karst channels, noted as the epiflow, may be greater (or even much greater) than the spring discharge.
5.5. Remarks on the recharge of the low conductivity volumes: the "Faraday cage" effect of epikarst
The huge low permeability fractured limestone volumes are often designated as the "capacitive" part of karst aquifers. They might contain important groundwater resources, and their recharge mechanism may have important practical consequences on the groundwater management problems (base-flow of karst springs, exploitation of groundwater by pumping wells or galleries, etc.).
Fig. 19a ("deep" karst syncline) and Fig. 19b ("shallow karst") suggest that a well developed epikarst layer enhancing the concentrated infiltration into the high conductivity karst channel network will "short-circuit" the low conductivity volumes and will play the role of a "Faraday cage" with respect to the main aquifer. Depending on the importance of this "Faraday cage" effect, the recharge of the low conductivity volumes could be much smaller than in the case of pure diffuse infiltration, with the above mentioned important consequences on the ground-water management problems. In the "deep syncline" configuration the inversion of gradients will always contribute to recharging the low conductivity volumes "from the interior", but in the "shallow karst" configuration the "short-circuit" of the low permeability volumes might be almost total.
6. Conclusion and outlook
Karst aquifers are 3-D systems and cannot be reduced to 2-D objects without losing important information on the infiltration processes and the distribution of hydraulic heads. Numerical experiments with 2-D and 3-D finite element models using the combined discrete channel and continuum approach, and simulating the infiltration and groundwater flow processes in a highly simplified theoretical karst aquifer, allowed to show the role of the organized karst channel network and the importance of the existence or non-existence of an epikarst zone enhancing concentrated infiltration. The effect of the epikarst on the hydraulic head and the groundwater flow field has practical consequences on the monitoring strategies applied for karst aquifers, on the interpretation of the global responses obtained at the karst springs and on the estimation of the recharge of the low conductivity "capacitive" volumes. Hydraulic head measurements should always be related to zones of known hydraulic conductivity and the "piezometric maps" of karst aquifers should always indicate the hydraulic conductivity at the measurement points (see, for example, Jeannin 1995).
In a quite general way, it should be examined whether the presently available observations allow to solve the problems which we meet in karst hydrology or not. Indirect estimation of the hydraulic parameter fields, interpolation or extrapolation of the available data are important problems in the practice. A good genetic theory would be, perhaps, the best "interpolation function", but the elaboration of such a theory would require common research between specialists of groundwater flow and specialists of karst evolution.
Acknowledgements
Some of the computer codes used for the groundwater flow simulation and some of the ideas presented in this paper were developed in the framework of earlier research projects supported by the Swiss National Foundation for Scientific Research. Our most sincere thanks to this Institution.
References
- Ababou R., Trégarot G. and Larabi A. 1998. Partially Saturated Hydrological Flows: Numerical Experiments and Analyses. Proceedings IXth CMWR, Computational Methods in Water Resources, Crete, Greece, June 1998, 8 pp.
- Barton N. (coordinator). 1978. Suggested methods for the quantitative description of discontinuities in rock masses. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts 15(6), 319-368.
- Bear J., Tsang C.F. and de Marsily G. (Eds.). 1993. Flow and contaminant transport in fractured rock. San Diego: Academic Press.
- Bedinger M.S. 1966. Electric analog study of cave formation. Nat. Speleol. Soc. Bull. 28 (3), 127-132.
- Berkaloff E. 1967. Limite de validité des formules courantes de tarissement de débit. Chronique d'Hydrogéologie 10, 31:41.
- Bonacci O. 1987. Karst Hydrology. Berlin: Springer Verlag.
- Bonacci O. 1993. Karst springs hydrographs as indicators of karst aquifers. J. Hydrol. Sciences 38(1-2), 51-62.
- Bonnet M., Margat J. and Thiery D. 1976. Essai de représentation du comportement hydraulique d'un système karstique par modèle déterministe: application à la "Fontaine de Vaucluse". Annales scientifiques de l'Université de Besançon, fasc. 25, 3e série, 79-95. Deuxième colloque d'hydrologie en pays calcaire.
- Burger A. 1956. Interprétation mathématique de la courbe de décroissance du débit de l'Areuse, Jura neuchâtelois (Suisse). Bull. Soc. Neuch. Sc. Nat. 79, 49-54
- Chinnery M.A. 1965. Secondary faulting. 1. Theoretical aspects. Canadian Journ. Earth Sci. 3, 163-174.
- Dreiss S.J. 1982. Linear kernels for karst aquifers. Water Resour. Res. 18 (4), 865-876.
- Dreiss S.J. 1989. Regional scale transport in a Karst aquifer: 1. Component separation of spring flow hydrographs. Water Resources Research 25 (1), 117-125.
- Drogue C. 1967. Essai de détermination des composantes de l'écoulement des sources karstiques. Chronique d'Hydrogéologie 10, 42-47.
- Drogue C. 1972. Analyse statistique des hydrogrammes de décrues des sources karstiques. J. Hydrol. 15, 49-68.
- Eisenlohr L., Kiraly L., Bouzelboudjen, M. and Rossier Y. 1997. Numerical simulation as a tool for checking the interpretation of karst spring hydrographs. J. Hydrol. 193, 306-315.
- Forkasiewicz J. and Paloc H. 1967. Le régime de tarissement de la Foux de la Vis. Chronique d'hydrogéologie 10, 59:73
- Fritz P., Cherry J.A. Weyer K.U. and Sklash M. 1976. Storm runoff analyses using environmental isotopes and major ions. In: "Interpretation of environmental isotope and hydrochemical data in groundwater hydrology", IAEA, p. 111-130.
- Gramberg J. 1965. The axial cleavage fracture. 1. Axial cleavage fracturing, a significant process in mining and geology. Engineering Geology 1(1), 31-72.
- Gu W.Z. 1992. Challenge on some rainfall-runoff conceptions traced by environmental isotopes in experimental catchments. In: Hoetzl and Werner (Eds.), Tracer Hydrology. p. 397-403.
- Harum T. and Fank J. 1992. Hydrograph separation by means of natural tracers. In: Hoetzl and Werner (Eds.), Tracer Hydrology. p. 143-146.
- Hauns M., Jeannin P.-Y. and Hermann F. 1998. Tracer transport in karst underground rivers: tailing effect from channel geometry. Bull. Centre d'Hydrogéol. 16, 123-142.
- Helmig R. 1993. Theorie und Numerik der Mehrphasenströmungen in geklüftet-porösen Medien. Institut für Strömungsmechanik und Elektron. Rechnen im Bauwesen der Universität Hannover, Bericht Nr 34/1993, 186 p.
- Hobbs S.L. and Smart P.L. 1986. Characterisation of carbonate aquifers: a conceptual base. Proc. 9th Int. Congr. of Speleology, Barcelona.
- Irons B.M. 1970. A frontal solution program for Finite Element analysis. Int. Journ. Num. Meth. Eng. 2, 5-32.
- Jeannin P.-Y. and Grasso A. 1995. Recharge respective des volumes de roche peu perméable et des conduits karstiques, rôle de l'épikarst. Bulletin du Centre d'Hydrogéologie 14, 95-111.
- Jeannin P.-Y. and Maréchal J.-C. 1995. Lois de pertes de charge dans les conduits karstiques: base théorique et observations. Bulletin du Centre d'Hydrogéologie 14, 149-176.
- Jeannin P.-Y. 1995. Comportement hydraulique mutuel des volumes de roche peu perméable et des conduits karstiques: conséquences sur l'étude des aquifères karstiques. Bulletin du Centre d'Hydrogéologie 14, 113-148.
- Jeannin P.Y. and Sauter M. 1998. Analysis of karst hydrodynamic behaviour using global approaches: a review. Bull. Centre d'Hydrogéologie 16, 31-48.
- Jamier D. and Simeoni G. 1979. Etude statistique de la distribution spatiale des éléments structuraux dans deux massifs des Alpes helvétiques: conséquences pour l'hydrogéologie karstique. Bulletin du Centre d'Hydrogéologie 3, 1-26.
- Kiraly L. 1969. Anisotropie et hétérogénéité de la perméabilité dans les calcaires fissurés. Eclogae Geol. Helv. 62/2, 613-619.
- Kiraly L. 1973. Notice explicative de la carte hydrogéologique du canton de Neuchâtel. Supplément du Bulletin de la Société neuchâteloise des sciences naturelles, Tome 96, 16 p. + carte.
- Kiraly L. 1975. Rapport sur l'état actuel des connaissances dans le domaines des caractères physiques des roches karstiques. In: Burger A. and Dubertret L. (Eds), Hydrogeology of karstic terrains, Int. Union of Geol. Sciences, B, 3, 53-67.
- Kiraly L. 1978. La notion d'unité hydrogéologique. - Bulletin du Centre d'Hydrogéologie 2, 83-216.
- Kiraly L. 1979. Remarques sur la simulation des failles et du réseau karstique par éléments finis dans les modèles d'écoulement. Bulletin du Centre d'Hydrogéologie 3, 155-167.
- Kiraly L. 1984. Régularisation de l'Areuse (Jura suisse) simulée par modèle mathématique. In: Burger A. and Dubertret L. (Eds), Hydrogeology of karstic terrains, Int. Union of Geol. Sciences, B, 3, 94-99.
- Kiraly L. 1985. FEM301 - A three dimensional model for groundwater flow simulation. NAGRA Technical Report 84-49, 96 p.
- Kiraly L. 1988. Large scale 3-D groundwater flow modelling in highly heterogeneous geologic medium. In: Custodio E. et al. (Eds.), Groundwater flow and quality modelling, NATO ASI series Vol.224, 761-775.
- Kiraly L. 1994. Groundwater flow in fractures rocks: models and reality. 14. Mintrop Seminar über Interpretationsstrategien in Exploration und Produktion, Ruhr Universität Bochum 159/1-21.
- Kiraly L., Mathey B. and Tripet J.-P. 1971. Fissuration et orientation des cavités souterraines: région de la Grotte de Milandre (Jura tabulaire).- Bull. Soc. Neuchâteloise Sc. Nat. 94, 99-114.
- Kiraly L. and Morel G. 1976a. Etude de régularisation de l'Areuse par modèle mathématique. Bulletin du Centre d'Hydrogéologie 1, 19-36.
- Kiraly L. and Morel G. 1976b. Remarques sur l'hydrogramme des sources karstiques simulé par modèles mathématiques. Bulletin du Centre d'Hydrogéologie 1, 37-60.
- Kiraly L. and Mueller I. 1979. Hétérogénéité de la perméabilité et de l'alimentation dans le karst: effet sur la variation du chimisme des sources karstiques. Bulletin du Centre d'Hydrogéologie 3, 237–285.
- Kiraly L., Perrochet P. and Rossier Y. 1995. Effect of the epikarst on the hydrograph of karst springs: a numerical approach. Bulletin du Centre d'Hydrogéologie 14, 199-220.
- Klemes V. 1986. Dilettantism in hydrology: transition or destiny? Water Resources Research 22 (9), 177S-188S.
- Klimchouk A.B., Ford D.C., Palmer A.N. and Dreybrodt W. (Eds.). 2000. Speleogenesis. Evolution of karst aquifers. Nat. Spel. Soc., Huntsville, Alabama, USA.
- Labat D. 2000. Nonlinéarité et nonstationarité en hydrologie karstique. Ph.D. thesis at Université de Toulouse, IMFT.
- Lee C.H. and Farmer I. 1993. Fluid flow in discontinuous rocks. London: Chapman & Hall, 169 p.
- LeGrand H.E. and Stringfield V.T. 1966. Development of permeability and storage in the Tertiary limestones of the south eastern states, USA. Bull. AIHS 11 (4), 61-73.
- Mandel S. 1966. A conceptual model of karstic erosion by groundwater. Bull. AIHS XI/1, 5-7.
- Mangin A. 1975. Contribution à l'étude hydrodynamique des aquifères karstiques. Thèse, Université de Dijon, 124 p.
- Mangin A. 1984. Pour une meilleure connaissance des systèmes hydrologiques à partir des analyses corrélatoire et spectrale. J. Hydrol. 67, 25-43.
- Martinec J., Siegenthaler U., Oeschger H. and Tongiorgi E. 1974. New insights into the runoff mechanism by environmental isotopes. In: Isotope techniques in groundwater hydrology, IAEA-SM-182/9, 129-143.
- Martinec J., Oeschger H., Schotterer U., Siegenthaler U., Nuti S. and Tongiorgi E. 1979. Example of separation of runoff components by environmental isotopes. Rivista Italiana di Geofisica e Scienze Affini 5, 87-89.
- Martinec J., Oeschger H., Siegenthaler U., Schotterer U., Nuti S. and Tongiorgi E. 1979. Example of a separation of runoff components by environmental isotopes. Rivista italiana di geofisica e scienze affini, vol 5, 87-89.
- Martinec J., Oeschger H., Schotterer U. and Siegenthaler, U. 1982. Snowmelt and groundwater storage in an Alpine basin. In: Hydrological Aspects of Alpine and High Mountain Areas, IAHS Publ. No 138, 169-175.
- Mohrlok U. 1996. Parameter-Identifikation in Doppel-Kontinuum-Modellen am Beispiel von Karstaquiferen. Dissertation an der Geowissentschaftlichen Fakultät der Universität Tübingen, TGA, Reihe C, Nr. 31, 125 p.
- O.E.C.D. 1988. The International HYDROCOIN Project. Level 1: code verification. OECD Publications, Paris, 198 p.
- Rhodes R. and Sinacori M.N. 1941. Pattern of ground-water flow and solution. J. of Geology 49 (8), 785-794.
- Romm E.S. and Pozinenko B.V. 1963. Investigation of seepage in fractured rocks. Trudy VNIGRI, No. 214, Leningrad. (in Russian).
- Rouleau A. 1985. Statistical characterization and numerical simulation of a fracture system. Application to groundwater flow in the Stripa granite. Ph.D. thesis, University of Waterloo.
- Scheidegger A.E. 1963. The physics of flow through porous media. University of Toronto Press.
- Schoeller H. 1967. Hydrodynamique dans le karst. - Chronique d'Hydrogéologie 10, 7-21.
- Snow D.T. 1969. Anisotropic permeability of fractured media. Water. Res. Research 5 (6), 1273-1289.
- Swinnerton A.C. 1949. Hydrology of limestone terrains. In: Meinzer O.E. (Ed.), Hydrology, Physics of the Earth. New York: Dover Publ.
- Toth J. 1963. A theoretical analysis of groundwater flow in small drainage basins. J. Geophys. Res. 68, 4798-4812.
- Trégarot G. 2000. Modélisation couplée des écoulements à saturation variable avec hétérogénéités, forçages et interfaces hydrologiques. Thèse de doctorat de l'INP de Toulouse. Institut de Mécanique des Fluides de Toulouse, Mai 2000.
- Tripet J.-P. 1972. Etude hydrogéologique du bassin de la source de l'Areuse. Mat. carte géol. de la Suisse, série Hydrologie, 21, 183 p.
- Trösch J. and Zurbrügg C. 1995. Turbulent flow in high permeable karst. Bulletin du Centre d'Hydrogéologie 14, 235-240.
- Wollrath J. and Helmig R. 1991. SM-2, Strömungsmodell für inkompressible Fluide, Theorie und Benutzerhandbuch. Institut für Strömungsmechanik, Universität Hannover, Techn. Bericht 1991.