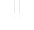(1) University of Bremen, Germany. E-mail: This email address is being protected from spambots. You need JavaScript enabled to view it.
(2) Karst Research Institute ZRC SAZU, Postojna, Slovenia. E-mail: This email address is being protected from spambots. You need JavaScript enabled to view it.
Abstract
Karst aquifers in their initial state consist of a net of fractures with largely differing aperture widths. As a most simple example we investigate the evolution of a karst aquifer where a wide fracture with aperture width A0 = 0.03 cm is embedded into a dense net of narrow fractures of aperture widths a0 < A0. The aim of this work is to investigate the influence of the hydraulic coupling between these fractures to the evolution of the karst aquifer. The modelling domain consists of a confined aquifer, which is divided into a square network consisting of narrow fractures. In its center a straight wide fracture leads from the input at hydraulic head h to the output at head zero. We have computed the breakthrough times of this aquifer as a function of a0. For a0 = 0 the breakthrough time is that of an isolated one-dimensional fracture. As a0 is increased the breakthrough times drop until at about a0 > 0.02 cm they are reduced significantly by almost one order of magnitude. This is caused by the following mechanism. As the central tube gets enlarged into a funnel like shape from its entrance water from its tip is injected into the fine net of fractures. Therefore more aggressive solution enters into the central fracture and enhances dissolutional widening there. By this way aquifers with wide fractures embedded into a continuum of fine fractures experience accelerated karstification.
Keywords by authors: karst, modelling, evolution, dual aquifer, limestone dissolution
Introduction
Karst aquifers due to their complex structure respond in an unexpected way to drawdown of groundwater, rain storms or input of pollutants. In order to facilitate risk assessment with respect to geohazards detailed information on their hydrological properties is of utmost importance. The ultimate aim of karst modeling is to construct a virtual aquifer with properties known in detail such that its reactions to external natural or anthropogenic perturbations can be studied. This work is an attempt into this direction. It deals with the evolution of a simple idealized karst aquifer, which in its initial state consists of a net of narrow fractures into which a wider fracture is embedded. The interaction of flow in this fracture with the continuum has a significant impact on its dissolutional widening and consequently on the evolution of the aquifer. In an earlier study Bauer et al. (2000) reported on a similar scenario, where a tube is embedded into a continuum with known conductivity. This concept, however, is incomplete since dissolutional widening is active only in the tube and the continuum of fractures remains unaffected. This work, which avoids this deficiency, was initiated by workshops of the modeling groups of Bremen, Neuchâtel, and Tübingen in spring 2000 and 2001 where differing concepts in karst modeling were discussed.
Model structure
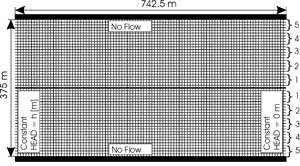
The idealized model aquifer, depicted in Fig. 1, consists of a limestone bed 1 m in depth, 742.5 m long and 375 m wide. It is dissected by fractures into blocks of 7.5 x 7.5 x 1 m3. The aperture widths of all narrow fractures are equal in scenario A, but log normally distributed in scenario B. They are varied from 10-5 cm to 0.03 cm in different computer runs. Along the center of the aquifer a wider fracture with aperture width of 0.03 cm extends from the left hand boundary with a constant head h to the output at head zero. The upper and lower boundaries are impervious. Flow through the fractures is calculated from mass conservation stating that total inflow and total outflow into each node must balance. For laminar flow, as checked by Reynolds number below 3000, the relation between flow rate Q and hydraulic head h is given by the Hagen-Poiseuille-equation, whereas for turbulent flow the Darcy-Weisbach equation is used. The friction factor in turbulent flow is calculated by employing the Colebrook-White formula (Dreybrodt, 1988). Details of the numerical calculations can be taken from Siemers and Dreybrodt (1998) for laminar flow, and from Clemens et al. (1996) for turbulent flow.
The water entering into the fractures at the high head boundary is highly aggressive to calcite. It has low calcium concentration, c = 0, and the capability to dissolve ![]() mol/l of calcite to attain equilibrium.
mol/l of calcite to attain equilibrium.
Fig. 1. Model domain with geometry of continuum fractures. The central fracture is shown by the solid line. The brackets indicate regions as discussed in the text.
Dissolutional widening is effective in all fractures of the system by the particular dissolution kinetics of limestone, which is linear for calcium-concentrations below 0.9 ![]() and then switches to a nonlinear behaviour of fourth order. Details can be taken from Dreybrodt and Eisenlohr (2000). Rate constants employed here are k1 =
and then switches to a nonlinear behaviour of fourth order. Details can be taken from Dreybrodt and Eisenlohr (2000). Rate constants employed here are k1 = ![]() and k4 =
and k4 = ![]() mmol
mmol ![]() .
.
The scenario is typical for the early evolution of karst, when sufficient amounts of water are available to maintain the head. As the fractures widen flow increases and by a positive feedback loop a dramatic increase of flow causes a breakthrough event (Dreybrodt 1996, Dreybrodt and Gabrovsek, 2000). The runs are terminated at a flow rate of 0.5 ![]() . Thereafter a constant recharge boundary condition must be used.
. Thereafter a constant recharge boundary condition must be used.
Results
In the first set of scenarios A and B the head at the input is chosen as 100 m. This is extremely high and related to situations as they occur on dam sites in karst regions. The model domain then corresponds to a bed of karstifiable rock extending below the dam. Fig. 2 depicts the evolution of flow through the exit of the wide center fracture for various values of the fracture aperture widths in the continuum for scenario A. In all cases flow increases slowly until a dramatic increase occurs which marks breakthrough. Fig. 3 demonstrates these breakthrough times as a function of the fracture aperture widths of the continuum. For very low values the central fracture is isolated because exchange of flow between this fracture and the continuum can be neglected. The breakthrough time therefore is close to that of a single isolated fracture. As the fracture aperture widths of the continuum increase the central fracture loses flow into the continuum. As a consequence the flow of aggressive solution into its input increases and breakthrough time is reduced. When all fractures have even aperture widths of 0.03 cm flow is directed along each fracture and exchange of flow between them is excluded. Therefore each fracture behaves like a single isolated fracture and they all have common breakthrough. This explains the behaviour of breakthrough times in Fig. 3. For scenario B breakthrough times are almost identical.
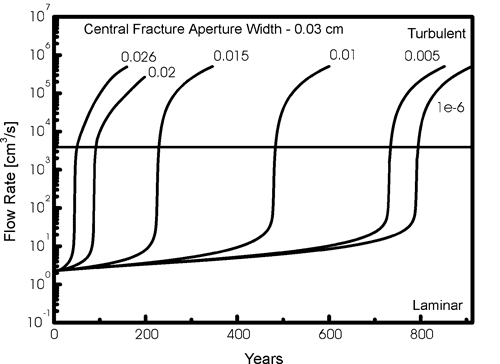
Fig. 2. Scenario A: Flow rates through the central conduit as a function of time. The numbers on the breakthrough curves denote the aperture widths of the continuum fractures. The horizontal line separates the regions of laminar and turbulent flow.
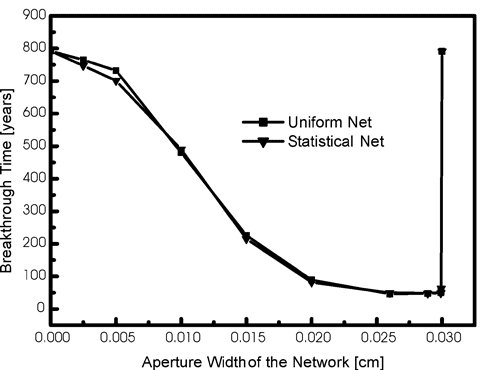
Fig. 3. Breakthrough times for Fig. 2 as a function of aperture widths of the continuum fractures. ![]() scenario A,
scenario A, ![]() scenario B.
scenario B.
The evolution of the karst aquifer for both a continuum of equal aperture widths ![]() = 0.02 cm and for a continuum with log normally distributed widths with average
= 0.02 cm and for a continuum with log normally distributed widths with average ![]() = 0.02 cm and
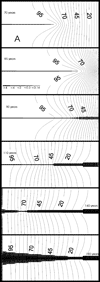
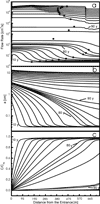
= 0.02 cm and ![]() = 0.01 cm is illustrated by Fig. 4. During the first 80 years a conduit propagates downstream along the central channel until breakthrough occurs after 90 years. From the head distribution one visualizes that flow is concentrated to the central conduit first and then enters into the continuum. This causes fast widening of neighbouring continuum fractures. After 90 years a fan starts to develop propagating uphead into the aquifer. After flow has become turbulent the pressure distribution changes and becomes more evenly distributed with higher gradients at the input. Therefore neighbouring fractures experience fast widening and now a fan of fractures expands downhead. The behaviour of the aquifer with statistically distributed aperture widths is similar but deviates in details. Due to the statistic distributed pathways with wider average aperture widths occur.
= 0.01 cm is illustrated by Fig. 4. During the first 80 years a conduit propagates downstream along the central channel until breakthrough occurs after 90 years. From the head distribution one visualizes that flow is concentrated to the central conduit first and then enters into the continuum. This causes fast widening of neighbouring continuum fractures. After 90 years a fan starts to develop propagating uphead into the aquifer. After flow has become turbulent the pressure distribution changes and becomes more evenly distributed with higher gradients at the input. Therefore neighbouring fractures experience fast widening and now a fan of fractures expands downhead. The behaviour of the aquifer with statistically distributed aperture widths is similar but deviates in details. Due to the statistic distributed pathways with wider average aperture widths occur.
Fig. 4. Evolution of conduits for scenarios A and B. The bar code for fracture widths in centimeters is shown in the second section of scenario A. The head distribution is illustrated by lines of constant head in steps of 5 m.
Therefore alternative small channels grow from the input. They cause a redistribution of heads towards the central conduit. This directs the growth of these channels towards the central conduit. Therefore a net of such conduits is integrated in addition.
The mechanisms determining the evolution of the aquifer are also reflected by the profiles of flow rate, aperture widths, and concentration along the central conduit. These are shown by Fig. 5 for scenario A at various times. We first discuss the evolution during the first 80 years. The profiles are depicted from 10 to 80 years in steps of 10 years. During this time the conduit propagates downhead and loses flow into the continuum. This can be seen from Fig. 5a, showing a significant decrease of flow rates at the not yet widened constriction of the central conduit. The location of this constriction is seen in Fig. 5b which shows the corresponding profiles of the aperture widths. The calcium concentrations illustrated by Fig. 5c increase linearly along the conduit until at its constriction they reach a stable value. This behaviour is in contrast to that of an isolated conduit, where the concentration rises steeply and attains a value close to equilibrium after a very short distance from the input at all times until breakthrough (Dreybrodt, 1996). The reason is that due to the loss of water into the continuum much more aggressive water flows into the central conduit. To show this difference we have performed at each timestep a calculation of the flow through the central channel, when all its connections to the continuum were cut. The full squares on the curves show the much smaller amount of flow. Only one point need to be given since for the central conduit isolated by this way flow remains constant along its length.
From 80 to 90 years the profiles are shown in steps of 2 years. During this time the exit opens quickly and a high amount of flow is lost into the continuum, where this attraction of flow with water of comparably low concentration creates the fan of parallel conduits. At 90 years flow becomes turbulent. The concentrations drop to low values along the entire conduit and dissolutional widening becomes even along the conduit. The profiles are shown in steps of ten years. The evolution of the fan which propagates uphead is reflected by the step like profiles which indicate loss of flow into these parallel conduits. At 140 years an increase of flow is observed at the input. It results from the fan propagating downhead. This fan grows quickly and after sufficient time conquers the entire domain.
This complex behavior of aquifer evolution occurs, when the aperture widths in the continuum are close to that of the middle fracture. If this is not the case the central fracture evolves as a single conduit. But, because of the low aperture widths in the continuum, dissolution is restricted such that the timescales of the evolution of the parallel fans are much longer than the time needed for the evolution of the central fracture. Shortly after breakthrough the condition of constant head breaks down. Therefore no time is left for the generation of conduits in the continuum.
Fig. 5. Profiles of a) flow rate, b) aperture widths and c) concentration along the central conduit at various times. See text.
We now turn to the case of low hydraulic head in the order of meters, to model natural karstification. In this case breakthrough times are significantly longer, in the order of ten thousands of years. We have performed runs for a head of 3 m leaving everything else unchanged for both the uniform and the statistical case. A channel propagates downhead and reaches the exit after 45000 years. After this breakthrough event concentration along this channel drops and widening is even and close to the maximal rates. The further time until breakdown of constant head conditions is too short to allow the evolution of a fan of conduits at the exit.
Discussion
We first consider the evolution of aquifers under extremely high hydraulic heads, e.g. dam sites. In Fig. 6 we have plotted the flow rates at the exit fractures for scenario A from Fig. 4. Curve 0 shows the evolution of flow rates in the central fracture. Curves 1 to 5 depict the flow which emerges from the segments 1 to 5 as illustrated by Fig. 1. During the first 80 years curves 1 to 5 are identical. This shows that flow is evenly distributed at the exits. One may also visualize this from the head distribution in Fig. 4. Most of this flow originates from flow through the central conduit, which is lost into the continuum (see Fig. 4a). This solution enters into the continuum with high calcium concentration and is not very effective to widen the fractures there. Enhancement of widening, compared to an isolated channel is effective only in the tube. Therefore one would expect that switching off dissolutional widening in the continuum will not change breakthrough time. We have performed such runs and indeed have found no change. We have to consider, however, that in scenario A all fractures have equal aperture widths. In case B with statistically distributed aperture widths the situation is similar during the first 70 years. Then the exit fan starts to develop due to alternative, more favourable pathways. Nevertheless, our results show that until close to breakthrough dissolutional widening in the continuum is not of significant importance in the evolution of the aquifer. Therefore in this time domain models which neglect widening in the continuum (Bauer et al., 2000) are acceptable approximations.
After breakthrough flow becomes turbulent and is concentrated to the central conduit and to the fan in section 1. There is only little flow in all the other sections, as illustrated by the steep drop of curves 1 to 5. This flow is laminar everywhere. As one can see from the pressure distribution from 110 to 140 years in Fig. 4, flow in the outer fractures is mainly directed along these and there is little exchange to neighbouring ones. Dissolutional widening is therefore slow in this region. The further behaviour is governed by dissolutional widening of the fractures close to the central region. It is obvious that this cannot be modelled if one neglects widening in the continuum.
Now we turn to the case of low hydraulic heads as usual in nature. Under such conditions dissolutional widening is restricted to the central channel. After breakthrough the time needed to create fans is much longer than the time available until the hydraulic head breaks down and further evolution is governed by constant recharge through the central channel. The reason for the different behaviour under high and low hydraulic heads results from the fact that dissolutional widening at the exit of a fracture is proportional to ![]() whereas flow is proportional to h (Dreybrodt, 1996, Dreybrodt and Gabrovsek, 2000). With n = 4, as used in our model runs, dissolutional widening at the exits drops by factor of 0.009 when the head changes from 100 m to 3 m. After breakthrough dissolution rates on the central conduit are maximal and even, independent of hydraulic head. By this way the time scales of evolution in the conduit and in the continuum of narrow fractures are similar under high heads but become significantly different when the head drops.
whereas flow is proportional to h (Dreybrodt, 1996, Dreybrodt and Gabrovsek, 2000). With n = 4, as used in our model runs, dissolutional widening at the exits drops by factor of 0.009 when the head changes from 100 m to 3 m. After breakthrough dissolution rates on the central conduit are maximal and even, independent of hydraulic head. By this way the time scales of evolution in the conduit and in the continuum of narrow fractures are similar under high heads but become significantly different when the head drops.
In summary we state that modelling of natural karst aquifers containing prominent fractures embedded into a continuum of narrow fractures shows an enhancement of karstification by loss of water from the prominent fractures into the continuum, and evolution of the aquifer proceeds by widening of the prominent fractures. In this case dissolutional widening in the continuum has little influence.
Under high hydraulic heads and moderate differences between the aperture widths of the prominent fractures and those of the continuum this is no longer the case. Especially when modelling the evolution of karst conduits below dam sites models neglecting dissolution in the continuum (Bauer et al, 1999) may underestimate risks.
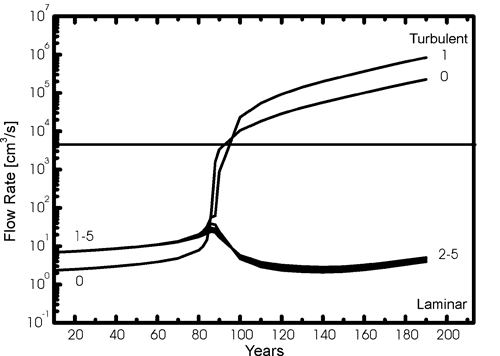
Fig. 6. Time dependence of flow rates at the exit of the central conduit (curve 0), and of the flow rates exiting from sections 1 to 5 as depicted in Fig. 1 (curves 1 to 5).
References
Bauer S., Liedl R. and Sauter M. 2000. Modelling of karst development considering conduit matrix exchange flow. In: F.Stauffer, W.Kinzelbach, K.Kovar, and E.Hoehn (Eds.), Calibration and reliability in ground water modelling. IAHS publication 265, 10-15.
Bauer S., Birk S., Liedl R. and Sauter M. 1999. Solutionally enhanced leakage rates of dams in Karst regions, In: A.N.Palmer, M.V.Palmer and I.Sasowsky D. (Eds.), Karst Modelling. Karst Water Institute, Special Publication 5.
Clemens T., Hückinghaus D., Sauter M., Liedl R. and Teutsch G. 1996. A combined continuum and discrete network reactive transport model for the simulation of karst development. In: Calibration and Reliability in Groundwater Modelling. IAHS Publ, 237, Colorado, pp. 309-318.
Dreybrodt W. 1988. Processes in karst systems – Physics, Chemistry and Geology. Springer: Berlin, New York, Heidelberg.
Dreybrodt W. 1996. Principles of early development of karst conduits under natural and man-made conditions revealed by mathematical analysis of numerical models. Water Resources Research 32, 2923-2935.
Dreybrodt W. and Eisenlohr L. 2000. Limestone dissolution rates in karst environments. In: A.Klimchouk, D.Ford, A.Palmer and W.Dreybrodt (Eds), Speleogenesis: Evolution of karst aquifers. Huntsville: Natl. Speleol. Soc., 136-148.
Dreybrodt W. and Gabrovsek F. 2000. Dynamics of the evolution of a single karst conduit. In: A.Klimchouk, D.Ford, A.Palmer, W.Dreybrodt (Eds), Speleogenesis: Evolution of karst aquifers. Huntsville: Natl. Speleol. Soc., 184-193.
Siemers J. and Dreybrodt W. 1998. Early development of karst aquifers in percolation networks of fractures in limestone. Water Resources Research 34, 409-419.