Department of Earth Sciences, State University of New York Oneonta. NY 13820-4015, USA.
E-mail: This email address is being protected from spambots. You need JavaScript enabled to view it.
Palmer, A.N. 2003. Patterns of dissolutional porosity in carbonate rocks. / Speleogenesis and Evolution of Karst Aquifers 1 (1), www.speleogenesis.net , 9 pages, re-published from: Palmer, A.N., Palmer, M.V., and Sasowsky, I.D. (eds.), Karst Modeling: Special Publication 5, The Karst Waters Institute, Charles Town, West Virginia (USA), 71-81.
Abstract: This paper reviews the hydrochemical processes that determine the patterns of caves and other solutional features within carbonate rocks. The model presented relies on the functional relationships expressed by chemical mass balances, flow equations, and kinetic expressions for dissolution rate. Although it shares many aspects of purely conceptual models and is backed by field evidence, its quantitative basis places it into the realm of analytical models.
The conclusions merely summarize earlier work (mainly Palmer, 1981, 1991. Solutional enlargement of caves and other karst features is highly selective in water that is close to equilibrium with dissolved carbonate minerals, enlarging only the most favorable openings – i.e. those that transmit the greatest discharge. This is characteristic of long flow paths within a typical karst aquifer. In contrast, solutional enlargement will be rather uniform along many competing flow paths where there is (1) high discharge, (2) sustained steep hydraulic gradients, (3) short flow paths, or (4) local renewal of aggressiveness by mixing, oxidation of sulfides, etc. These conditions produce maze caves and epikarstic networks. In general, this condition prevails if Q/rL > 0.001 cm/sec (tubes), or /bL > 0.001 cm/sec (fissures), where Q = discharge, r = tube radius, b = long dimension of fissure cross section, and L = distance of flow from where the initial aggressive solution comes in contact with the carbonate rock.
Introduction
Unlike most geologic processes, the origin of dissolution porosity lends itself readily to analytical solutions. Four salient "laws" govern the process: two mass balances (water balance and chemical mass balance) and two kinetic equations (which describe the dissolution rate and the flow rate of water), and in combination they provide a theoretical basis for quantifying the solutional history of karst aquifers. The greatest difficulty is in applying these clean-cut analytical tools to the complex and rather disordered world of geology. It is impossible to model a karst aquifer in all its details, because most of the details are unknown.
However, a great deal can be learned about the origin and distribution of dissolution porosity by using the analytical approach to obtain a battery of governing concepts that can be applied to all karst aquifers. This paper summarizes the evolution of a conceptual model whose details were first developed on the basis of field observation and hydraulics, and only later substantiated by chemical kinetics. It applies specifically to carbonate rocks, although the general approach can be modified to fit any geologic setting by substituting the appropriate expressions for kinetics and fluid flow.
General distribution of karst porosity
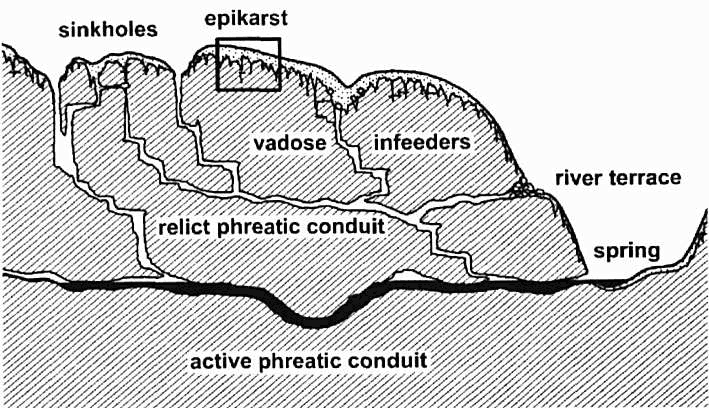
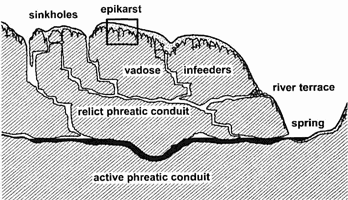
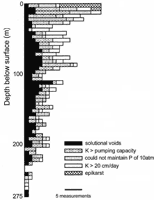
The appropriate first step relies on concepts that are well known to everyone. Water, where if first enters a soluble rock, is undersaturated with respect to the minerals in that rock. Its saturation ratio (C/Cs) with respect to these minerals is at, or close to, zero. (C = concentration of dissolved mineral, e.g. calcite; Cs = saturation concentration, which is greatly enhanced by acids. Cs for calcite in typical groundwater is about 2-3 mmol/L.) Dissolution is most rapid where C/Cs is lowest, and its rate diminishes as the dissolved load increases. The greatest dissolution occurs where the water first enters the soluble rock and diminishes with flow distance. Thus most of the water's solutional aggressiveness is usually squandered at and near the bedrock surface, simply lowering the surface and widening the upstream ends of fissures that penetrate the rock (Fig. 1). Underground water circulating through the rock has greatly diminished aggressiveness, but unless Cs decreases (e.g. by CO2 degassing, rising temperature, or common-ion effects) the water will never quite reach saturation. Since the flow of water is continuous from recharge source to outlet, and the relatively high C/Cs allows dissolution to proceed only at a slow rate, the dissolution porosity is drawn out along the entire length of the flow paths. Aggressiveness can be maintained by a gradual rise in Cs for example by oxidation of organic compounds. Aggressiveness can also undergo a local burst because of mixing of different waters or by oxidation of hydrogen sulfide. However, in a typical karst aquifer the solutional porosity tends to form continuous conduits rather than isolated voids (Fig. 1). The diminution of dissolution porosity with depth in karst aquifers is well documented by borehole data (Fig. 2).
Introductory geology textbooks typically portray karst porosity in cross sections that resemble blocks of Tilsit cheese, with the holes elongated along beds and fractures as a gratuitous nod to the influence of geology. This portrayal would be amusing, were it not for the fact that many scientists and engineers, perhaps subconsciously, use the same conceptual view of karst when attempting to solve environmental problems. The real distribution of karst porosity is more complex, but also more predictable.
Fig. 1. Generalized cross section of a karst aquifer formed by meteoric water, showing relative distribution of dissolution voids. The apparent porosity is exaggerated in the diagram for clarity. Below the epikarst the total dissolution porosity rarely exceeds a few percent and is commonly far less (see paper by Worthington in this volume).
Fig. 2. An example of the variation in karst porosity with depth, as observed in deep boreholes in Herzegovina (Modified from Milanovic, 1981).
Within karst aquifers, most of the dissolution porosity consists of conduits, usually arranged in dendritic patterns in which tributaries join each other to produce fewer but larger conduits in the downstream direction. When we visit a cave of this kind, our conception of dissolution porosity can easily be-skewed. The impression is that the overall dissolution porosity must be enormous. However, it is concentrated in only a relatively few conduits, which, if compared to the overall rock volume, yield only a tiny porosity, usually less than a percent (see Worthington, in this volume, for representative examples). In the most complex part of Mammoth Cave, Kentucky, Palmer (1995) calculated the total dissolution porosity to be only 4%, even though the figure includes many more inactive relict passages than active ones. Most accessible caves are surrounded by rock in which the vast majority of openings have hardly enlarged at all. The conduits are not surrounded by porous zones, with walls like a sponge, where progressively smaller openings extend indefinitely into the cave wall. The conduits are quite discrete.
As shown by the morphology of cave passages, the flow of aggressive water through karst aquifers takes place mainly along fractures and bedding-plane partings, and much less so along primary pores. It is important to note that fractures and partings diminish in width and number with depth (see Ford and Ewers, 1978, and Ford in this volume). Provided the openings are too small to admit turbulent flow, the flow is described by the Hagen-Poiseuille equation:
|
(1) |
where Q = discharge, w = fissure width, b = fissure breadth (long dimension of fissure cross section), ![]() = specific weight of water, µ = dynamic viscosity of water, and dh/dL = hydraulic gradient. Although groundwater can pass through all openings in varying amounts, note the strong dependence of flow on fissure width. Since w diminishes downward, one can assume that the water will preferentially follow shallow paths, far more so than in aquifers whose pore size does not decrease so significantly with depth (for example, gravel). This applies to fractured bedrock aquifers of all types, but especially in soluble rocks where the initial openings are enlarged by the flow. As these openings grow, some will enlarge more rapidly than others. They are the ones that grow to cave size and which eventually dominate the flow pattern within the aquifer. The onset of turbulent flow is often used to distinguish the birth of a karst conduit.
= specific weight of water, µ = dynamic viscosity of water, and dh/dL = hydraulic gradient. Although groundwater can pass through all openings in varying amounts, note the strong dependence of flow on fissure width. Since w diminishes downward, one can assume that the water will preferentially follow shallow paths, far more so than in aquifers whose pore size does not decrease so significantly with depth (for example, gravel). This applies to fractured bedrock aquifers of all types, but especially in soluble rocks where the initial openings are enlarged by the flow. As these openings grow, some will enlarge more rapidly than others. They are the ones that grow to cave size and which eventually dominate the flow pattern within the aquifer. The onset of turbulent flow is often used to distinguish the birth of a karst conduit.
This discussion applies mainly to phreatic water. Gravitational vadose water is easily perched for some distance on resistant or relatively insoluble beds, providing a strong lateral component to the flow, interrupted by shafts where the perching beds are breached by fractures.
The tendency for conduits not to penetrate far below the potentiometric surface is disrupted to some extent by faulting and folding. In tectonically disturbed areas it is possible for certain flow paths to extend to considerable depths, especially along faults. For example, in a catalog of solutional voids encountered beneath river beds during drilling by the Tennessee Valley Authority (Moneymaker, 1941), the deepest voids are encountered in the folded and faulted Appalachians and in the fault zone of western Kentucky. Ford (1971) emphasized low fissure frequency as the main criterion for why certain caves extend deep beneath the potentiometric surface, whereas Palmer (1969) emphasized fissure width. The two contrasting views are nevertheless compatible.
Despite this disruption, the shallowest paths are still the most favorable, even in tectonically disturbed areas, and deep conduits are relatively rare. Pervasive deep flow is likely only in confined settings, or where favorable stratigraphic boundaries allow deep dissolution (for example, along sulfate-carbonate interfaces). Worthington (1991) cites many examples of sulfate-rich springs fed by groundwater that follows deep basin-wide paths.
Rates of conduit growth
In a fissured aquifer with myriad flow paths, which ones are most likely to enlarge into solution conduits? This is not a trivial question, because the presence and distribution of conduits is one of the most important variables in the assessment of a karst aquifer. Phreatic conduits form potentiometric lows and are the main paths of groundwater discharge, as well as the major paths of contaminant transport. The configuration of vadose channels determines how sources at the surface relate to the points of recharge at the underlying water table.
In most carbonate aquifers only a small percentage of flow routes enlarge into turbulent-flow conduits. Early in the flow history of the aquifer, fissures are narrow and the flow is dispersed among many different routes, each with its own overall hydraulic gradient, mean fissure width, total flow length, and mean discharge. Groundwater discharge and velocity are so small that the water becomes nearly saturated with dissolved bedrock long before it emerges at the surface. This can be verified by measuring the chemistry of inflowing seepage through narrow openings into accessible caves. Even some substantial flows of several cm3/sec arrive essentially at C/Cs =1.0 after less than 50 m of flow. Therefore, in any single flow route, the rate of dissolutional enlargement depends simply on the chemical mass balance. The mass of material removed from the walls of the opening is equal to the mass removed in solution by the groundwater flow. This rule is independent of the shape of the opening (tube, fissure, etc.).
The chemical mass balance can be stated as follows: Mass removed from the walls of the opening = mass carried away in solution. Change in mass with time = ![]() , where
, where ![]() = rock density,
= rock density, ![]() = change in volume with time, and
= change in volume with time, and ![]() = change in dissolved load over the length of the conduit. A conduit of circular cross section is assumed for convenience; the actual conduit shape is not important, since the functional relationships are the same. Thus, within any single conduit segment of rather uniform dimensions, the rate of wall retreat (S) can be stated
= change in dissolved load over the length of the conduit. A conduit of circular cross section is assumed for convenience; the actual conduit shape is not important, since the functional relationships are the same. Thus, within any single conduit segment of rather uniform dimensions, the rate of wall retreat (S) can be stated
|
(2) |
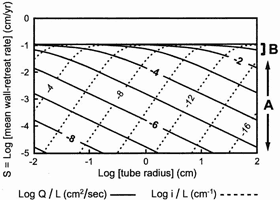
Fig. 3. Mean rate of wall retreat (cm/yr) as a function of discharge (Q), flow distance (L,), hydraulic gradient (i), and tube radius (r) in tubular conduits at 10° C and PCO2 = 0.01 atm (CS = 212 mg/L CaCO3). Values of i/L are valid only for laminar flow. A = region of varied growth rates (Q/rL < 0.001 cm/sec); B = maximum possible solutional growth rate, limited by chemical kinetics. (From Palmer, 1981).
where C0 = initial concentration of dissolved bedrock (mg/L), r = conduit radius (cm), and L = conduit length (cm). All other terms are in cgs units. The numerical coefficient converts the result to cm/yr. A uniform radius is not required, since we are concerned only with mean values of S, Q, and r, and again the functional relationships are not affected.
Early in the evolution of a karst aquifer, when the water emerges from each opening essentially at saturation, if we assume that C0 = 0, then ![]() = CS, which is constant at a given temperature and CO2 partial pressure. Under these conditions, the mean rate of wall retreat within each conduit is therefore a linear function of Q/rL.
= CS, which is constant at a given temperature and CO2 partial pressure. Under these conditions, the mean rate of wall retreat within each conduit is therefore a linear function of Q/rL.
The mean S values plot as the family of lines shown in group A of Fig. 3 (10° C, PCO2 = 0.01 atm). At any value of r, the larger the Q/L ratio, the greater the rate of enlargement. Large Q and/or small L favor rapid enlargement. Dashed lines show the corresponding values of i/L, where i = hydraulic gradient, are also shown on Fig. 3, valid only for laminar flow (derived from the tubular version of eq. 1, where ![]() is replaced by
is replaced by ![]() ).
).
The numerical values for S in Fig. 3 are misleading, because (1) they assume that the water enters each conduit at zero saturation; (2) most of the dissolution is concentrated in the upstream end of the conduit, so that the rate throughout the majority of the conduit is less than the mean; and (3) they do not consider mixing or branching between different conduits. However, it is the relative values - the general relationships among the terms - that concern us here, not the specific numerical values. Actual growth rates are best determined with finite-difference calculations or analytical methods (e.g. Palmer, 1984, 1991;Dreybrodt, 1990,1996; Groves and Howard, 1994a and b; Clemens et al, 1996; Hanna and Rajaram, 1998).
The earliest conduit growth usually begins somewhere in (or beyond) the lower left portion of Fig. 3. Growth rates are far too low to allow turbulent-flow conduits to develop in a geologically feasible time. Within any given conduit, the growth rate can increase only if Q increases, since L does not change. If Q does not increase, the enlargement rate will remain static or actually decrease, as shown by the negative slope of the lines in group A as the conduit radius increases. (Conduits of non-circular cross section would have more gently sloping lines in group A.)
But the growth rate reaches an upper limit beyond which it cannot rise. This is typically about 0.001-0.01 cm/yr, depending on the chemical conditions. So far the analysis has been focused on narrow openings in which the water emerges near saturation. Now consider a conduit with such a large Q/L ratio that water is able to pass through the conduit while retaining nearly all its aggressiveness. The entire conduit enlarges at a nearly uniform rate (shown as B in Fig. 3), which is a function of the dissolution kinetics, rather than of the mass balance. Rates of wall retreat are almost uniform and independent of Q/L.
Experiments by Berner and Morse (1974), Plummer and Wigley (1976), Plummer et al. (1978) show that in turbulent flow the dissolution rate for calcite is governed mainly by the chemical reactions at the wall, rather than by mass transfer within the fluid, and that turbulence and flow velocity have little effect on. Mass transfer does have an effect at low flow rates in limestone conduits (Curl, 1968; Buhmann and Dreybrodt, 1985a and b, Dreybrodt, 1988), and in evaporites at any flow rate, but the pattern of lines in group A in Fig. 3 is not affected.
For carbonate rocks, the dissolution rate is expressed by
|
|
(3) |
where ![]() = surface area of rock in contact with water, V = water volume, k = reaction coefficient, and n = reaction order. It is more common for the parenthetical term to be expressed as (CS - C), but the form shown in eq. 3 avoids the problem of having to adjust the units of k whenever n changes. Values of k and n depend on the acid content of the water (for example, PCO2), and k also varies with temperature and lithology (Palmer, 1991, derived from the original lab measurements of Plummer et al., 1978, Plummer and Wigley, 1976, Rauch and White, 1977, and other sources). The reaction order (n) increases rather abruptly from 1-2 to 4 or more at C/CS values that range from about 0.6 to 0.9, depending on temperature and PCO2 (Palmer, 1991; Dreybrodt et al. in this volume). In typical groundwater, n = 2 (or 1, in narrow conduits) and k = 0.01 at C/CS <=0.65. At greater C/CS n=4 (occasionally more; see Dreybrodt et al., 1999) and k = 0.1.
= surface area of rock in contact with water, V = water volume, k = reaction coefficient, and n = reaction order. It is more common for the parenthetical term to be expressed as (CS - C), but the form shown in eq. 3 avoids the problem of having to adjust the units of k whenever n changes. Values of k and n depend on the acid content of the water (for example, PCO2), and k also varies with temperature and lithology (Palmer, 1991, derived from the original lab measurements of Plummer et al., 1978, Plummer and Wigley, 1976, Rauch and White, 1977, and other sources). The reaction order (n) increases rather abruptly from 1-2 to 4 or more at C/CS values that range from about 0.6 to 0.9, depending on temperature and PCO2 (Palmer, 1991; Dreybrodt et al. in this volume). In typical groundwater, n = 2 (or 1, in narrow conduits) and k = 0.01 at C/CS <=0.65. At greater C/CS n=4 (occasionally more; see Dreybrodt et al., 1999) and k = 0.1.
Because C/CS < 1, an increase in reaction order represents a decrease in dissolution rate. Ironically, this decrease appears to be essential to the origin of nearly all solution conduits (Palmer, 1984). If the low-order (rapid) kinetics were to prevail throughout the initial opening, virtually all the aggressiveness would be consumed within a few meters of flow, except in usually wide fissures, and the growth rate would be so slow in the rest of the conduit that it would never achieve turbulent flow within a geological feasible time. On the other hand, the high-order (slow) kinetics alone are too slow to enlarge the conduits to the size of traversable caves. White (1977) called the change from slow to rapid dissolution a "kinetic trigger" that represents the beginning of true cave development. Thus cave origin enjoys the best of both worlds: slow growth when the aggressiveness must persist for long distances through narrow fissures, and later rapid growth to achieve large size.
Combining eqs. 2 and 3, and substituting ![]() and
and ![]() , gives the following general equation for dissolutional wall retreat in carbonate rocks:
, gives the following general equation for dissolutional wall retreat in carbonate rocks:
|
|
(4) |
which is valid for all types of flow and conduit geometries (Palmer, 1991). The maximum rate of wall retreat (aside from occasional mechanical erosion during floods in large conduits) can be determined by this equation, where C/CS = saturation ratio where the water enters the conduit. In Fig. 3, the maximum rate at B is for C/CS = 0. Higher saturation ratios, even as high as 0.9, still provide enlargement rates that are rapid by geological standards, and the overall shape of the graph in Fig. 3 remains valid.
The composite graph in Fig. 3 shows both the early laminar flow (S dependent on Q/L) and the late-stage flow (S independent of Q/L). The curvature of the lines where Zone A meets Zone B was determined by finite-difference analysis.
It is not realistic to assume that water can pass through an entire aquifer without changing its saturation ratio. The water acquires most of its solute load at the upstream end, especially where it accumulates in small openings that feed the main conduits. The maximum enlargement rate in a conduit is thus limited in part by the value of C0 at its upstream end, which is rarely less than 0.5. High-Q flow can pass through a cave-size conduit for great distances while gaining only a few mg/L of dissolved load. Because of the large Q, this still represents a substantial rate of mass flux.
Competition between enlarging flow paths: unitary conduits and branchworks
The specific configuration of conduits within the aquifer is determined by the relative growth rates of competing flow paths. The most common situation, where meteoric groundwater passes through a carbonate unit from an upland recharge surface to outlets at lower elevation, can be described as follows:
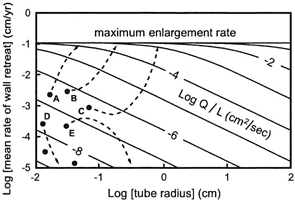
1. Early in the flow history of the aquifer, the many alternate flow routes have low Q/L ratios and plot in or beyond the lower left comer of Fig. 3. Their Q/L values and rates of conduit growth span a wide range of many orders of magnitude. All growth rates are small, but some will be much greater than others. The dots on Fig. 4 show some representative flow paths early in the aquifer development. These are idealizations, because no single flow path behaves entirely independently.
2. Growth rate can increase only if the Q/L ratio increases. For any given path, this can be achieved only by an increase in discharge. As each opening grows, its discharge tends to increase because more water is able to pass through. But there is a maximum amount of available infiltration, and eventually a conduit can acquire additional Q only at the expense of its neighbors. This is achieved in two ways: (a) As a conduit grows, its hydraulic head decreases (despite increasing Q) because of the reduced amount of head loss required to transmit the flow. Water is drawn from neighboring openings in which the head is greater, which increases the discharge in the major conduits, (b) Sinkholes develop as the major openings and their tributaries enlarge, especially at the upstream ends, funneling water into the largest conduits but bypassing lesser openings. As a result, the openings with the largest initial Q/L or i/L are those that are most likely to acquire increasing flow and to increase their enlargement rate. As shown by the arrows in Fig. 4, some openings are favored over their neighbors and increase rapidly in both Q and S. Others languish with negligible and generally decreasing Q and S.
Fig. 4. Varied growth histories of competing flow paths in the early stages of a karst aquifer. Paths A, B, and C accelerate in growth and reach the maxium rate by increasing their discharge. These are the routes that become major dissolution conduits. In contrast, other paths (e.g. D and E) stagnate at low and usually diminishing enlargement rates.
3. Enhanced discharge is able to increase the enlargement rate only up to a certain point, beyond which the rate becomes insensitive to further increases in Q. The enlargement rate is now limited mainly by the dissolution kinetics. Those relatively few conduits that reach this state grow at approximately the same rapid rate, with only minor differences caused by local variations in chemistry, flow, and passage configuration. Traversable caves are formed by water that has achieved this state.
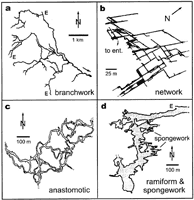
Single-passage stream caves and branchwork caves are the normal result. Branching caves are by far the most common, because of the tendency for convergence of flow toward the relatively low head of the major conduits, and because of fortuitous intersections between passages. The typical passage pattern is similar to that in Fig. 5a. This example is located in prominently bedded, low-dip strata. Greater structural complexity leads to comparable passage complexity, but the overall cave pattern is usually a branchwork.
Uniform dissolution among many competing flow routes: labyrinthine porosity
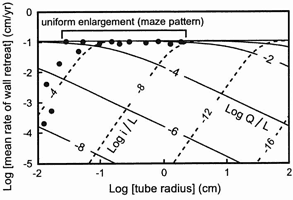
Under certain conditions, nearly every competing flow route enlarges at comparable rates, and a labyrinth of interconnected openings is formed. According to Fig. 3, the only way this can happen is to expose many openings simultaneously to high values of Q/L or i/L. Beyond a certain threshold (Q/rL > 0.001 cm/sec in tubes, Q/bL>0.001 cm/sec in fissures), they will all enlarge at rather similar rates, regardless of size, discharge, gradient, or flow length. The result is a labyrinth of interconnected passages consisting of openings that have grown simultaneously to cave size. Caves formed under these conditions have maze patterns (Fig. 5 b, c, and d). Favorable conditions include the following:
Where aggressive water first enters the soluble rock (small values of L). Distances of flow from the entry points are short, and all openings have large Q/L values regardless of opening size or discharge. The most common example is the epikarst, the zone of extensive dissolution in the upper few meters or tens of meters of the soluble rock, located either beneath a soil cover or exposed directly at the surface (Fig. 1). The same approximate result is achieved where water passes through a porous, non-soluble rock before entering the carbonate rock, forming a maze cave. Network caves formed along intersecting fractures are the most common type (Figure 5b). The flow of water can be downward from the overlying surface or upward as artesian flow from an underlying formation (provided the water has not encountered substantial amounts of carbonate rock beforehand).
Fig. 5. Examples of solutional cave patterns: (a) Crevice Cave, Missouri, (b) part of Crossroads Cave, Virginia, (c) part of Holoch, Switzerland, (d) main rooms of Carlsbad Cavern, New Mexico. Maps courtesy of Paul Houck, H.H. Douglas, Alfred Bogli, and Cave Research Foundation, respectively. E = entrance.
It is also possible to enlarge many alternate flow routes simultaneously where steep hydraulic gradients are imposed by flooding. This is most noticeable where soluble rock is exposed adjacent to entrenched rivers that flood severely. Water enters the ground as bank storage having high i/L ratios because of the steep gradients and short flow distances. The same effect is achieved in local areas within preexisting caves where flow constrictions (breakdown, sediment fill, interference by relatively insoluble beds) cause floodwater to pond upstream from them. Seasonal or storm-related flooding periodically injects aggressive water into every available opening, enlarging them rapidly and simultaneously. Irregular network caves (western part of Fig. 5b) are formed where vertical or steeply inclined fractures dominate. Anastomotic caves are formed where bedding-plane partings or low-angle faults are the main cave-forming units. Where matrix porosity provides the major flow paths, for example in diagenetically young limestones, breccias, or reef rock, a spongework pattern will form (as illustrated in parts of Fig. 5d).
Fig. 6. Many alternate routes are able to enlarge simultaneously at roughly the same rate, regardless of size, if they are all able to sustain high discharges (e.g. because of steep hydraulic gradients) or short flow distances. Maze caves, epikarst, and pervasive labyrinthine porosity are produced in this way. Very small openings, or those with low Q/L or i/L will not be competitive.
Where steep hydraulic gradients are sustained (e.g. beneath dams), growth rates rise steeply in all conduits as r increases, as shown by the dashed lines in Fig. 3, until they all reach the maximum rates of wall retreat at or near the top of the graph. A network of similarly enlarged conduits is expected (Palmer, 1988; Dreybrodt, 1996; Bauer et al, 1999).
Solutional aggressiveness can be renewed in zones of mixing between chemically contrasting waters, for example between infiltrating high-CO2, freshwater and low-CO2 seawater. Local network and spongework patterns are produced, not only because the flow distances from the source of aggressiveness are short, but because of the diffuse nature of most water flow under these circumstances. Carbonate aquifers in coastal and island settings are noted for this kind of porosity (Back and others, 1984; Mylroie and Carew, 1990; Mylroie and Vacher, 1999).
Mixing between rising (often thermal) waters and meteoric water is capable of producing considerable aggressiveness. Caves formed in this way tend to have network or irregular ramiform patterns (Fig. 5 b and d). Oxidation of rising hydrogen sulfide rising from depth into oxygen-rich zones at or near the water table produces a burst of localized dissolution. This process usually results in network and ramiform caves, consisting of large irregular rooms with sequential branches exiting to the surface (Fig. 5d). The outflow usually coalesces into discrete conduits as aggressiveness is lost and flow length increases.
Summary
This simplified view of the distribution of karst porosity leads to several conclusions, which are summarized below:
Karst porosity is greatest near the land surface in areas of groundwater recharge (for example, in the epikarst). It diminishes in the downflow direction but coalesces into relatively few major conduits that are continuous through the entire aquifer. Except in mixing or redox zones, karst porosity rarely occurs as isolated voids. Branching conduit patterns are the most common.
Conduits form only where the setting is favorable for certain flow paths to gain discharge at the expense of their neighbors, e.g. by development of sinkholes.
Dissolution labyrinths, in which every accessible opening is enlarged to comparable amounts, form in several settings: (a) within short distances of flow from where aggressive water first enters a soluble rock, or where mixing or redox reactions produce local zones of undersaturated water within a karst aquifer; (b) in areas of steep hydraulic gradient, where Q/L and i/L are large.
Dissolution porosity diminishes greatly at depths beneath the local base level because of the very strong influence of fissure widths on resistance to flow.
Use of these concepts can aid in the prediction of porosity distribution and geometry. However, it must be recognized that relict karst porosity can also occur where conditions favorable to its origin are no longer present. Also, details of geologic structure must be considered. These ideas are developed further in the literature.
The concepts described here have not changed significantly since their first brief publication in 1981, although they have been explored at greater length since by more advanced geochemical and digital models (see Palmer, 1991 and 1995). The model described in Fig. 3 was generalized from the behavior of individual conduits. However, subsequent digital modeling of multiple-conduit networks has validated these concepts.
References
Back W., Hanshaw B. and Van Driel J.N. 1984. Role of groundwater in shaping the eastern coastline of the Yucatan Peninsula, Mexico. In: LaFleur, R. G. (Ed.): Groundwater as a geomorphic agent, Boston, Mass..Alien and Unwin, Inc., 281-293.
Berner R.A. and Morse J.W. 1974. Dissolution kinetics of calcium carbonate in sea water, IV: Theory of calcite dissolution. American Journal of Science 274, 108-134.
Buhmann D. and Dreybrodt W. 1985a. The kinetics of calcite solution and precipitation in geologically relevant situations of karst areas. 1: Open system. Chemical Geology 48, 189-211.
Buhmann D. and Dreybrodt W. 1985b, The kinetics of calcite solution and precipitation in geologically relevant situations of karst areas. 2: Closed system. Chemical Geology 53, 109-124.
Clemens T, Huckinhaus D., Sauter M., Liedl R. and Teutsch G. 1996. A combined continuum and discrete network reactive transport model for the simulation of karst development. In: Calibration and reliability in groundwater modeling. Proceedings of the ModelCARE 96 Conference held at Golden, Co., Sept. 1996: UAGS Publ. No. 237.
Curl R.L. 1968. Solution kinetics of calcite. Proceedings of 4th International Congress of Speleology, Ljubljana, Slovenia, 61-66.
Dreybrodt W. 1988. Processes in karst systems: physics, chemistry and geology: Berlin, Germany, Springer-Verlag, 288 p.
Dreybrodt W. 1990. The role of dissolution kinetics in the development of karst aquifers in limestone: a model simulation of karst evolution: Journal of Geology 98 (5), 639-655.
Dreybrodt W. 1996. Principles of early development of karst conduits under natural and man-made conditions revealed by mathematical analysis of numerical models: Water Resources Research 32, 2923-2935.
Ford D.C. 1971. Geologic structure and a new explanation of limestone cavern genesis: Transactions of the Cave Research Group of Great Britain 13 (2), 81-94.
Ford D.C., and Ewers R.O. 1978. The development of limestone cave systems in the dimensions of length and depth: Canadian Journal of Earth Sciences 15, 1783-1798.
Groves C.G., and Howard A.D. 1994a. Minimum hydrochemical conditions allowing limestone cave development. Water Resources Research 30 (3), 607-616.
Groves C.G., and Howard A.D. 1994b. Early development of karst systems, 1. Preferential flow path enlargement under laminar flow. Water Resources Research 30 (10), 2837-2846.
Hanna R.B., and Rajaram H. 1998. Influence of aperture variability on dissolutional growth of fissures in karst formations. Water Resources Research 34 (11), 2843-2853.
Milanovic P.T. 1981. Karst hydrogeology. Littleton, Colorado, Water Resources Publications, 434 p.
Moneymaker B.G. 1941. Subriver solution cavities in the Tennessee Valley. Journal of Geology 49, 74-86.
Mylroie J. E., and Carew J.L. 1990. The flank margin model for dissolution cave development in carbonate platforms: Earth Surface Processes and Landforms 15, 413-424.
Palmer A.N. 1969. A hydrologic study of the Indiana karst: Ph.D. thesis, Indiana Univ., Bloomington, Ind., 181 p.
Palmer A.N. 1981. Hydrochemical controls in the origin of limestone caves. 8th International Speleological Congress, Proceedings, Bowling Green, Kentucky, p. 120-122.
Palmer A.N. 1984. Recent trends in karst geomorphology. Journal of Geological Education 32, p. 247-253.
Palmer A.N. 1988. Solutional enlargement of openings in the vicinity of hydraulic structures in karst regions. Association of Ground Water Scientists and Engineers, 2nd Conference on Environmental Problems in Karst Terranes and their Solutions, Proceedings, p. 3-15.
Palmer A.N. 1991. Origin and morphology of limestone caves. Geological Society of America Bulletin, 103, 1-21.
Palmer A.N. 1995. Geochemical models for the origin of macroscopic solution porosity in carbonate rocks. In: D.A. Budd, Harris, P.M. and Sailer, A. (Eds.), Unconformities in carbonate strata: their recognition and the significance of associated porosity. American Association of Petroleum Geologists, Memoir 63, p. 77-101.
Plummer L.N., and Wigley T.M.L. 1976. The dissolution of calcite in CO2-saturated solutions at 25° C and 1 atmosphere total pressure. Geochimica et Cosmochimica Acta 40, p. 191-202.
Plummer L.N., Wigley T.M.L. and Parkhurst D.L. 1978. The kinetics of calcite dissolution in CO2-water systems at 5° to 60° C and 0.0 to 1.0 atm CO2. American Journal of Science 278, p. 179-216.
Rauch H.W, and White W.B. 1977. Dissolution kinetics of carbonate rocks. 1. Effects of lithology on dissolution rate. Water Resources Research 13, p. 381-394.
White W.B. 1977. Role of solution kinetics in the development of karst aquifers. In: Tolson J.S. and Doyle F.L. (Eds.), Karst hydrogeology. International Association of Hydrogeologists, 12th Memoirs, p. 503-517.
Worthington S.R.H., 1991. Karst hydrogeology of the Canadian Rocky Mountains. Ph.D. dissertation, McMaster University, Hamilton, Ont, 227 p.