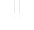Department of Earth Sciences, State University of New York, Oneonta, NY 13820, USA
Re-published by permission from: Gabrovsek, F. (Ed.), Evolution of karst: from prekarst to cessation. Postojna-Ljubljana, Zalozba ZRC, 43-60.
Abstract This paper outlines the current views on cave origin in carbonate rocks, combining ideas from a variety of sources. A typical dissolution cave develops in several stages that grade smoothly from one to the next: (1) Initial openings are slowly enlarged by water that is nearly at solutional equilibrium with the local bedrock. (2) As the early routes enlarge, those with the greatest amount of flow grow fastest. (3) These favoured routes eventually become wide enough that groundwater is able to retain most of its solutional aggressiveness throughout the entire distance to the spring outlets. This breakthrough time usually requires times on the order of 104 to 105 years and ends the inception phase of speleogenesis. (4) Discharge along these selected routes increases rapidly, allowing them to enlarge into cave passages rather uniformly over their entire length. Maximum enlargement rates are roughly 0.001-0.1 cm/yr, depending on the local water chemistry and lithology. (5) The cave acquires a distinct passage pattern that depends on the nature of groundwater recharge, the geologic setting, and the erosional history of the region. Branchwork patterns dominate in most carbonate aquifers. Maze caves are produced by any of the following: steep hydraulic gradients (e.g. during floods), short flow paths, uniform recharge to many openings, and mixing of waters that contrast in chemistry. (6) Enlargement rate usually decreases as passages become air-filled, owing to loss of aggressiveness as carbon dioxide escapes through openings to the surface. (7) The cave typically evolves by diversion of water to new and lower routes as the fluvial base level drops. (8) The cave is eventually destroyed by roof collapse and by intersection of passages by surface erosion. At any given time, different parts of the same cave may be experiencing different stages in this sequence.
Introduction
Caves are present in all rather pure carbonate rocks that are in geologic settings and climates that allow abundant groundwater recharge. For this reason, it is clear that cave origin requires no special chemical mechanism beyond the circulation of meteoric groundwater. Dissolution caves can form by other processes, but this is the common speleogenetic mode in most carbonate aquifers and is the main topic of this paper. Most of the concepts presented here are not new, but, where possible, alternate viewpoints are given in the hope of encouraging further discussion.
Cave inception
Speleogenesis requires one basic thing: Groundwater must dissolve the bedrock rapidly enough to produce caves before the rock is removed by surface erosion. This requires the through-flow of large amounts of solutionally aggressive water along stable flow paths.
The earliest stages
At great depth beneath the surface there is very little groundwater flow because openings in the rock are narrow and few, and hydraulic gradients are feeble. But as uplift and erosion expose these rocks near the surface, increasing amounts of groundwater pass through them. Along any given flow path, the solutional enlargement rate is controlled by a simple mass balance. The mass removed from the walls of the growing conduits is equal to that which is carried away in solution. The increase in volume thus depends on how much water passes through the conduit, and how rapidly the water dissolves the rock. In other words, the two major controls are discharge and chemical kinetics.
Early in the development of a carbonate aquifer, all groundwater becomes nearly saturated with dissolved calcite and/or dolomite before it emerges at the surface. The total amount of rock removed along any flow path is nearly independent of chemical kinetics, because the water has enough time to equilibrate with the rock, regardless of dissolution rates. The saturation concentration depends on the minerals present, CO2 concentration, type of system (open vs. closed), temperature, and interactions with other dissolved components. All these show considerable variation, both spatially and temporally, but it is unlikely that there will be major differences between neighboring flow paths within a given aquifer. In contrast, there are great variations in discharge from one flow path to another – and this is the main control over which the early paths are able to grow into caves.
Most dissolution takes place at the upstream ends of the flow paths, where aggressive water first enters the carbonate rock. (“Upstream” and “downstream” in the following discussion refer to the up-gradient and down-gradient ends of the system, even where the flow is only laminar seepage.) With time and distance, there is an increase in saturation ratio of the dissolved minerals (actual concentration divided by saturation concentration, C/Cs). At first the dissolution rate decreases in a roughly linear manner. But as the saturation ratio rises above approximately 60-90% (the exact value depends on temperature and CO2 content), the dissolution rate decreases much more rapidly. The result is that the final approach toward saturation is very slow (see Berner and Morse, 1974; Plummer and Wigley, 1976; Plummer et al., 1978; Dreybrodt, 1990; Palmer, 1991).
Dissolution is so rapid in the upstream sections that if the remainder of the dissolution followed the same trend, the water would lose virtually all its aggressiveness after only a short distance of flow. Dissolution would be so slow in the rest of the aquifer that cave development would be almost impossible (Palmer, 1984). Except in the most ideal situations (wide, short fractures with steep hydraulic gradients, e.g. along escarpments), enlargement of the initial openings to cave size would require many millions of years, during which the carbonate rock is likely to be entirely removed by erosion.
Interestingly, it would be unlikely for caves to form with either the rapid dissolution at low saturation ratios or the slow dissolution at high saturation ratios. Early slow dissolution along the entire flow path is essential for preparing the way for the rapid dissolution that follows. But the slow dissolution alone cannot enlarge the routes rapidly enough to form caves within a geologically feasible time. Rapid dissolution at low saturation ratios is necessary to achieve this. But, as shown above, the rapid dissolution by itself cannot form caves in most situations.
Geological aspects of cave inception
The initial width of fissures (e.g. fractures and partings) is perhaps the most uncertain of all field conditions that influence cave inception. By the time a cave is large enough for humans to enter, the evidence has long disappeared. Initial fissure width is a slippery concept, because the widths increase with time even without being dissolved, simply by release of stress as the overlying rocks are eroded away. Field evidence suggests that a minimum initial fissure width of about 0.01 mm is required for cave development (Bocker, 1969). However, this value depends on hydraulic gradient, flow distance, water chemistry, and length of time available, and so the threshold for initial fissure width is not a fixed value, but instead depends on the local setting.
To clarify how wide the initial fissures in limestone might be, it is helpful to gather data from relatively insoluble rocks that are approximately as brittle as limestone. Intrusive igneous rocks such as granite should give a close approximation. Water wells in these rocks have fairly small yields, especially at depths of more than 50 m below the surface (Freeze and Cherry, 1979, p. 158). But even with conservative estimates for hydraulic gradient and fissure frequency, the observed well yields require fissures that are roughly 0.1-0.5 mm wide. Surely only a few of the many fissures are this large, but they are important ones, which in soluble rock would grow into caves.
Inception horizons were originally defined by Lowe (1992) as beds or stratal interfaces that provide a chemical environment that favours cave development. The presence of pyrite along a geologic contact was cited as a typical example, whereby oxidation of the sulphide to sulphuric acid might give a substantial boost to cave development. One difficulty with this particular example is the deficiency of oxygen in most deep groundwater. Structural and hydraulic factors are also crucial in determining which initial openings are able to develop into caves.
The presence of interbedded sulphates within carbonate rocks provides a suitable environment for cave inception. Dissolution of the sulphates can boost porosity, although this process forces calcite to precipitate by the common-ion effect. Because of differences in molar volume, the precipitated calcite usually does not occupy all the porosity generated by dissolution of gypsum or anhydrite. This process is even more potent when limestone, dolomite, and gypsum interact within the same system. As calcite is forced to precipitate, the solubility of gypsum rises to almost 1.5 times more than that of gypsum alone, and the solubility of dolomite rises to several times its normal value. Because dolomite dissolves so slowly, the process is drawn out over long distances and times, potentially resulting in long, continuous paths of increased porosity that may pave the way for later cave development. The geochemical process has been validated by field measurements (e.g. Bischoff et al., 1994), but its impact on cave development is still unclear.
Breakthrough
Eventually the entire length of an incipient cave becomes large enough to allow water to pass all the way through while still retaining most of its aggressiveness. At this time there is a fairly sudden transition (“breakthrough”) to rapid dissolution throughout the entire flow path. From then on, the entire route enlarges rapidly at a roughly uniform rate of about 0.001-0.01 cm/yr, depending on the water chemistry. This rate varies with the amount of turbulence, but only at low saturation ratios (Plummer and Wigley, 1976; White, 1984). At the high saturation ratios of most karst water the effect is minor. In mature caves, abrasion by coarse sediment load can increase local rates of cave development (Smith and Newson, 1974). These factors are insignificant compared to the truly great differences in growth rate that distinguish true cave passages with low saturation ratios from narrow flow paths whose water is nearly saturated with dissolved carbonates.
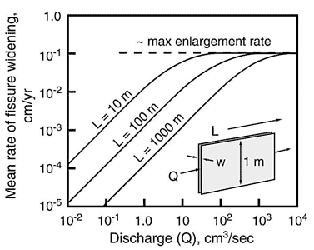
Fig. 1 shows the mean enlargement rate in an ideal fissure as a function of discharge and flow length. The steep parts of the curves represent the slow dissolution rates governed by the mass balance, and the horizontal segments at the top represent the rapid dissolution controlled mainly by kinetics (Palmer, 1991). Because the enlargement rates are not uniform throughout the fissure, the rates shown in Fig. 1 cannot be translated directly into the time required for an incipient cave to reach breakthrough. To do this, finite-difference modelling is necessary. The results are shown in Fig. 2.
The time required for chemical breakthrough can be considered the “gestation time” through which an incipient cave must pass in order to allow it to grow into a true cave. It is difficult to specify exactly when this time begins. In some ways, it involves the entire age of the carbonate aquifer, if one includes all the effects of early diagenesis, burial, and uplift in order to reach its present state (Klimchouk and Ford, 2000). But before cave growth can truly begin, there must be a substantial hydraulic gradient. Thus it is customary to start the clock when the carbonate rock is first exposed above base level, at the time when both recharge zones and discharge zones are well defined. Computer models can track the growth of idealized fissures of specified initial width, length, hydraulic gradient, and chemical attributes. These show that the breakthrough time is approximately proportional to w-3 (i/L)-1.4 P-1, where w = initial fissure width, i = mean hydraulic gradient, L = flow distance, and P = initial PCO2 (Palmer, 1988, 1991). Dreybrodt (1996) provided an analytical derivation arriving at nearly the same functional relationships.
Fig. 1. Mean enlargement rate of a fissure in limestone, as a function of discharge (Q) and flow length (L). Q = discharge per metre of fissure height (long dimension of fissure cross section). Assumptions include closed conditions, T = 10o C, initial PCO2 = 0.01 atm. (See Palmer, 1991.)
Fig. 2. Approximate breakthrough times for cave incep-tion along fissures in limestone. The main part of the graph shows closed conditions at T = 10o C and initial PCO2 = 1%. Variation of breakthrough time with initial fissure width, temperature, and initial PCO2 are shown. The combined variable i/L represents the hydraulic gradient (?h/L) divided by flow distance (L). Modified from Palmer (1991). See also Dreybrodt (1996).
Laminar discharge through the fissure is proportional to w3 i, which is essentially the inverse of two of the most important variables that determine breakthrough time. Thus the paths that develop most rapidly into caves are those with high discharge and short flow distance. High PCO2 is also favourable, as long as CO2 is not lost by degassing.
Temperature plays a complex role in determining how long it takes for breakthrough to occur. Higher temperatures speed the chemical reactions, but in long flow systems this can increase the breakthrough time by depleting most of the water’s solutional capacity in the upstream parts, leaving less for the downstream parts. High temperature increases the flow velocity by reducing the viscosity of the water, but it also decreases the amount of limestone or dolomite that can be dissolved. The net result is an increase in breakthrough time with rising temperature. However, another complication is that in warmer climates the CO2 production in the soil is greater, which shortens breakthrough times.
As shown in Fig. 2, breakthrough time decreases as much as 5 times if the CO2 consumed by carbonate dissolution is quickly replaced, for example when the water is in close contact with a CO2 source such as soil. This is rare. In general, the early phase of growth takes place in an approximately closed system, where CO2 is used up as dissolution proceeds. In caves with open atmospheres, CO2 is likely to be lost by air exchange with the surface, which more than offsets the apparent advantage of the open system.
Fig. 2 shows that initial fissures 0.01-0.1 cm wide would require no more than a few thousand or tens of thousands of years to reach the maximum enlargement rates, from the time aggressive groundwater first begins to flow through the limestone. For example, in a fissure 1 kilometre long, with an initial width of 0.02 cm, hydraulic gradient of 0.02 (20 m/km), PCO2 of 0.05 atm, temperature of ![]() C, and closed to further uptake of CO2, the maximum rate of enlargement is reached in about 30,000 years. These conditions are typical, perhaps even conservative. Lab work and computer modelling by Dreybrodt (1990, 1996) suggest even shorter breakthrough times that are probably more valid. Acids can also be generated within passages by oxidation of organic compounds in the water or iron sulphide in the bedrock, diminishing the breakthrough times. Water chemistry and flow vary with the seasons, but their effects average out over the years.
C, and closed to further uptake of CO2, the maximum rate of enlargement is reached in about 30,000 years. These conditions are typical, perhaps even conservative. Lab work and computer modelling by Dreybrodt (1990, 1996) suggest even shorter breakthrough times that are probably more valid. Acids can also be generated within passages by oxidation of organic compounds in the water or iron sulphide in the bedrock, diminishing the breakthrough times. Water chemistry and flow vary with the seasons, but their effects average out over the years.
Time required for a cave to reach traversable size
Beyond the breakthrough time, growth rate of a cave depends chiefly on the nature of its water input. In dense, rather pure limestone, the rate of wall retreat (S) can be estimated with the equation
![]()
where C/Cs is the saturation ratio, k is a reaction coefficient, and n is the reaction order (see Palmer, 1991 for units and further details). Values for k and n vary with PCO2, and k also varies with temperature. For quick applications, some representative averages can be given. At C/Cs < ~0.7, k and n are approximately 0.015 and 1.7 respectively. At C/Cs > ~0.7, k and n are roughly 0.24 and 4 respectively. Because (1-C/Cs) is less than 1, the larger exponent gives a smaller value of S.
For example, water that collects on insoluble rock and then flows as a sinking stream directly into a limestone cave usually has a ![]() of about 0.001-0.005 atm. This value is higher than that of the outside atmosphere (0.00036 atm) because even though the stream is open to the atmosphere, it acquires CO2 from seepage that enters the stream through the soil. At ponors, most sinking streams have saturation ratios of about 0.1-0.5. Under these conditions, limestone surfaces in the cave will dissolve as fast as 0.15 cm/yr. Ideally, a water-filled cave can increase its diameter up to 2-3 m in 1000 years. (The diameter increases at twice the rate of wall retreat, S.) Measurements with dial micrometers, repeated over several years, have verified these rates in caves fed by sinking streams (High, 1970; Coward, 1975).
of about 0.001-0.005 atm. This value is higher than that of the outside atmosphere (0.00036 atm) because even though the stream is open to the atmosphere, it acquires CO2 from seepage that enters the stream through the soil. At ponors, most sinking streams have saturation ratios of about 0.1-0.5. Under these conditions, limestone surfaces in the cave will dissolve as fast as 0.15 cm/yr. Ideally, a water-filled cave can increase its diameter up to 2-3 m in 1000 years. (The diameter increases at twice the rate of wall retreat, S.) Measurements with dial micrometers, repeated over several years, have verified these rates in caves fed by sinking streams (High, 1970; Coward, 1975).
In contrast, many caves are fed by water that infiltrates through soil and reaches the caves only after having traveled for a considerable distance along the soil-limestone contact and through narrow fissures in the epikarst. This water has a high PCO2 (about 0.01-0.05 atm) but has a high saturation value, usually about 0.75-0.95 by the time it reaches the caves. The diameter of a water-filled passage grows no more than about 20 cm per 1000 years under those conditions.
Organization of conduits
It has been shown that caves in a typical karst aquifer are able to form only along flow paths that increase their discharge with time. This can be achieved in either of two ways:
- By increasing the flow efficiency in a system with a fixed head difference. An example is leakage of water from a stream or other body of water that drains to a lower outlet. As the initial fissures widen, the discharge rises dramatically. The upstream head begins to decrease only when the conduit becomes large enough to transmit the entire stream flow. By that time breakthrough has already taken place.
- By increasing the catchment area that feeds an incipient cave passage. At first, water drains into the growing caves as widely dispersed seepage. Dolines form by subsidence into the rapidly growing voids at the soil/bedrock interface. As dolines increase their catchment area, their mean-annual discharge increases to the caves that they feed. Discharge to the caves increases in an irregular manner, much less rapidly than in routes fed by leaking streambeds, and hydraulic gradients decrease with time, even during the earliest periods of growth.
The difference between these two systems is important. Because the routes fed by surface streams can increase their flow much more rapidly, they are usually the first parts of a cave to form. Passages fed by depressions of limited catchment area require longer times to form, and they usually join the earlier passages as tributaries of a branchwork system. The first passages to form in a cave are usually short and direct, except where short paths are prohibited by the geologic setting. With time, these early passages serve as low-head targets for passages having more remote recharge sources (Ford and Ewers, 1978; Ford et al., 2000).
Less time is required for a cave to grow in small steps (i.e. where new, relatively short upstream passages link to earlier downstream ones) than for a single long passage to form. This is partly due to the non-linear relation between breakthrough time and flow distance. Although the growth of any single passage propagates in the downstream direction, the overall system grows in the upstream direction, away from the springs, by addition of new passages (Ewers, 1982; Ford et al., 2000).
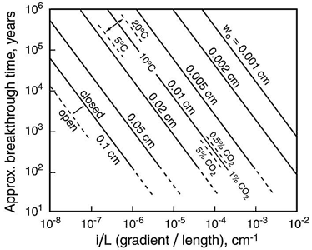
A typical sequence is shown in Fig. 3. Assume, for simplicity, that passage segments B-A and C-B have identical lengths and gradients. The breakthrough time for a single passage from C to A would be (LC-A / LB-A)1.4 longer than the breakthrough time for either of the two segments – i.e. about 2.6 times longer. This is 30% longer than it would take for segments B-A and C-B to reach breakthrough separately, one after the other. Just as importantly, the gradient of C-B would normally be less than that of B-A until the head dropped in B-A (Ford et al, 2000). The tributary from doline (D) has a smaller catchment area and is slower to reach cave dimensions.
Fig. 3. Evolution of a typical branchwork cave by successive piracy of sinking streams and development of recharge sources through dolines. Segment B-A forms first because of the short path length and steep gradient. Segment C-B links up later, aided by steepening of the gradient as segment B-A develops. (C-B does not necessarily join B-A at point B.) The passage from doline D is last to form because of its limited catchment area. See Ford and Ewers (1978) and Ford et al. (2000) for descriptions of hardware models that illustrate this concept.
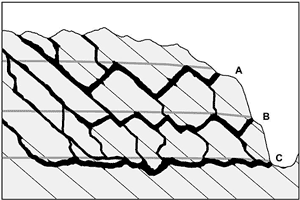
Since the flow of water through carbonate aquifers is controlled partly by the history of river entrenchment, the vertical arrangement of cave passages also reflects this control. The traditional view is that the largest passages are formed when base level is relatively static (Sweeting, 1950; Davies, 1960). At such times, rivers develop floodplains, and springs are held at fairly constant elevations for lengthy periods of time. Meanwhile the passages that feed the springs are able to grow large. In contrast, passages that form during rapid river entrenchment are usually small. The major passages form different levels, which in most cases decrease in age downward. Fluvial aggradation may cause some or all neighboring cave passages to fill with sediment over the vertical range of base-level rise.
This conceptual model has been well validated in Mammoth Cave, Kentucky (Palmer, 1989; Granger et al., 2001). However, in many caves there are several complications that disrupt this simple interpretation. Vadose passages may be perched on insoluble strata and grow to large size above base level. Most phreatic passages contain vertical loops that descend far below the local base level. Some phreatic caves follow favourable stratigraphic units such as zones of former sulphates. Even the ideal cave levels controlled by pauses in fluvial entrenchment are not perfectly “level”. For this reason, many people prefer to call them storeys or tiers, and either of these terms is preferred in general applications. However, the term cave level is still appropriate where there is a clear relation to fluvial base level. But the critical elevation is not the average elevation of a phreatic passage, but instead where there is a clear transition from vadose to phreatic morphology (for example, a transition from canyon to tube). This transition is not clear in some passages.
Fig. 4 is an idealized profile through a multi-storeyed cave, as described by Ford (1971). Three main stages of cave development are shown, with decreasing loop amplitudes from the highest storey to the lowest. This is not a characteristic of all multi-storeyed caves, but it is a conceptual ideal. Ford (1971) ascribed the decrease in amplitude to increasing fissure frequency in the host rock with time. Fissures are sparse at first, and passages are constrained to only a few deeply descending loops. As erosional unloading and cave development persist, fissures become more numerous until eventually the passages are able to form more or less along the water table, with minimal phreatic looping. In some caves the greater amplitude of loops in upper passages is instead caused by floodwaters, which superpose ungraded, looping bypass routes around low-flow routes that have more uniform gradients (Palmer, 1972). In the same vein, on the basis of studies in the Alps, Audra (1994) and Hauselmann et al. (2001) ascribe an epiphreatic origin to looping passages.
Fig. 4. Vertical layout of a typical cave, showing decreasing amplitude of phreatic loops with depth. This trend has been interpreted by Ford (1971) and Ford and Ewers (1978) to be the result of increasing fissure frequency with time. Successive positions of the water table are shown as gray lines. Some researchers consider these lines to represent the upper extent of epiphreatic flow (see text).
The earliest passages in a cave system (usually fed by sinking streams) may not show a clear distinction between vadose and phreatic development, because their discharge fluctuates a great deal, and because the initial potentiometric surface is relatively high. As a result, most of these passages are subjected to a variety of flow conditions – phreatic at first, and then vadose and epiphreatic at later times. Still, many of them show a fairly sharp transition from vadose canyons (with continuous downward trends) to phreatic tubes (with low gradients and usually irregular looping profiles). This transition is more sharply defined in secondary passages fed by karst depressions of limited catchment area, because the flow is more uniform with time and the water sources are usually well above the potentiometric surface.
Because of their gravitational flow, many vadose passages have a strong down-dip component, especially those in well-bedded rocks. Phreatic passages show no consistent relation to the dip, except where that is the only path to potential outlets, or where prominent fractures also extend in that direction. In well-bedded rocks, the intersection between the dipping beds and low-gradient water table encourage many phreatic passages to develop nearly along the strike of the beds. These relationships tend to be obscure where the geologic structure is complex.
Origin of branching systems
Branching cave patterns are by far the most common for several reasons:
• As passages enlarge, the local hydraulic head within them decreases. Groundwater flows from surrounding smaller openings, where the potentiometric surface is higher, toward the low heads of the early conduits.
• Vadose passages have no inherent tendency to converge, because they are hydraulically independent. However, the structures that they follow often intersect, forcing independent streams to join as tributaries. Examples include intersecting fractures, and synclinal structures in bedding-plane partings.
• Water from broad recharge areas converges toward outlets of limited extent, generally stream valleys, which causes a natural tendency for conduits to converge simply by competition for space. After two streams have converged, there is little opportunity for them to diverge farther downstream. The exception is in the vicinity of the spring outlet, where local distributary systems may develop because of collapse, backflooding, and widening of fissures by erosional stress release.
Maze development
Besides branchworks, most other caves are mazes in which all the passages form more or less simultaneously. A maze cave can form only if the growth rate is similar along many alternate flow paths. This can happen if all passages evolve simultaneously at the maximum rate shown in Fig. 1. If the ratio of discharge to flow distance (Q/L) is large in many alternate flow routes, they will enlarge at roughly the same rate (Palmer, 1991). Specifically, this condition is achieved if Q/rL > 0.001 (cgs units), where r = mean conduit radius. In fissures, this condition is reached if Q/bL > 0.001, where b = long dimension of the fissure cross section, perpendicular to the narrow dimension w. Specific settings where this condition is met include:
A. High-discharge or high-gradient flow during floods. Water is forced into all fissures in adjacent carbonate rocks under steep gradients, causing them to enlarge at approximately the maximum possible rate (Palmer, 2001). This process is most active in the vicinity of constrictions in the main stream passages, which result from collapse, sediment chokes, or poorly soluble strata.
B. Short flow paths from where the water first enters the soluble rock. Because of the short flow distances, all fissures except for the narrowest enlarge simultaneously at similar rates. The epikarst is an example. Network mazes are also formed by recharge through a permeable but insoluble material such as quartz sandstone (Palmer, 1975, 2000).
C. Uniform recharge to all fissures, regardless of their width. This can be achieved by seepage through porous, insoluble materials, as in B above.
D. Sustained high gradients, for example beneath dams.
E. Mixing zones, where the groundwater aggressiveness is locally boosted by mixing of waters of contrasting CO2 content or salinity, or by oxidation of sulphide-rich water. Over short flow distances, many alternate routes are enlarged. Mixing of waters of varied CO2 content can decrease breakthrough times, but large differences in CO2 concentration are necessary (Gabrovsek, 2000).
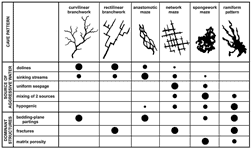
The differences in maze types depend partly on geologic structure. Network mazes consist of intersecting fissures, with a pattern resembling city streets. They require many intersecting fractures (joints or faults), which are typical of massive or thick-bedded rock. Most are formed by processes B, C, or E above. Anastomotic mazes have a braided pattern of intersecting tubes, usually arranged two-dimensionally along a single parting or fault. They are nearly all formed by process A above. Spongework mazes form where primary (matrix) porosity is dominant. In pattern they resemble the intersecting holes in a sponge. Most of them form by process E, and less commonly by process A. A two-dimensional variety can form along bedding-plane partings. Ramiform mazes consist of rooms with offshoots extending outward from them at various elevations. They usually include areas of network or spongework maze development and are formed mainly by process E. Many network and anastomotic mazes, and a few spongework mazes, are merely superimposed on a basic branchwork pattern and represent only part of the entire cave development.
Fig. 5 provides a summary of typical cave patterns, showing their relation to source of aggressive water and to dominant structural characteristics.
Supporting evidence from computer models
Finite-difference computer models support and clarify some of these relationships. Conspicuously absent from the list of ways to form maze caves is slow groundwater flow through artesian aquifers. This origin seems logical, and many maze caves are indeed located in aquifers that are partly artesian. However, artesian conditions by themselves do not produce maze caves. Modelling by Palmer (1991) showed that different-sized branches of a loop are least likely to enlarge at the same rate in slow-moving water near saturation. Dreybrodt and Siemers (2000) supported this idea by showing that as breakthrough time increases, passages tend to become unitary and exhibit less complexity. Modelling by Clemens et al. (1997) verified the development of network mazes by uniform seepage through an insoluble caprock, as described in B above. The insoluble cap encourages maze development because it is permeable, rather than a confining unit.
Conduit growth and modification
At the breakthrough time, when an incipient cave reaches its maximum growth rate, several other changes take place more or less simultaneously (White, 1977). The cave water changes from laminar to turbulent, which increases the solution rate slightly (see earlier discussion). The flow also becomes competent enough to transport detrital sediment. For example, it is able to carry away the soil that subsides into caves through karst depressions, allowing the depressions to grow more rapidly. The sediment load can also help to enlarge caves by mechanical abrasion, but, in places, sediment accumulates in thick beds that retard dissolution and erosion. Where sediment accumulates, upward dissolution by paragenesis is a possible consequence, especially in caves enlarged by periodic floodwaters. However, water within the sediment is often undersaturated and can still dissolve the underlying rock (Vaughan et al., 1998)
Fig. 5. Common patterns of solutional caves. Dot sizes show the relative abundance of cave types in each of the listed categories. Single-passage caves are rudimentary or fragmentary versions of those shown here.
When a cave is able to transmit the entire flow from its recharge area, the average flow can increase no further. Instead the head within the passage decreases as the cross section continues to enlarge. Much of the upstream part of the cave becomes vadose, and streams may entrench canyons in the passage floors.
As caves acquire entrances that allow air exchange with the surface, many free-surface cave streams lose part of their aggressiveness. Inflowing water is fairly rich in soil-derived CO2, and may acquire even more by oxidation of organic materials as it flows through the caves (Bray, 1972). Loss of CO2 through entrances and other openings can drive the stream water to supersaturation with dissolved calcite or dolomite, so that many vadose cave streams are aggressive only during high flow. Some vadose stream channels even acquire a thin coating of calcite in sections of supercritical flow during dry seasons. These deposits are usually removed during the following wet season, but with only a small net amount of solutional entrenchment each year. Measurements in caves of New York State show that the overall entrenchment rate of active stream canyons of this type can be as slow as 10-20 mm per thousand years (Palmer, 1996), despite the continuous flow of water. During six months of continuous monitoring in the largest stream in Mammoth Cave, Meiman and Groves (1997) found that 70% of the passage enlargement took place during the highest 7% of flow.
Dating of cave sediments by 26Al/10Be isotope ratios in quartz-rich cave sediment is a powerful tool for interpreting rates of cave development. Usually this sediment is deposited by the most recent active stream flow and gives a minimum age for the passage. At Mammoth Cave, 26Al/10Be dating suggests that the development of each passage level required at least 105 years (Granger et al., 2001). This value is compatible with the range of probable times required for breakthrough (Fig. 2) and for later enlargement to the present diameters of about 5-10 m in the major passages.
Headward erosion of resistant beds by cave streams can require a surprisingly long time. For example, sediment on ledges above an entrenched canyon in Mammoth Cave were dated at 1.13 million years, validated by samples at similar elevations elsewhere in the cave (Granger et al., 2001). The passage is floored by a metre-thick sequence of shaly and cherty limestone, which has been breached by a deep canyon that post-dates the sediment. Headward entrenchment has progressed only 360 m along the passage, and only about half of that has occurred upstream from the sampling site. The entrenching stream is still active today and is quite capable of transporting gravel. The rate of headward entrenchment appears to be less than half a metre per thousand years.
But under favourable conditions, diversion of passages from one level to another can take place rather rapidly. Post-glacial diversion of water in New York State caves has formed traversable passages up to a metre in diameter and 200 m long since the last glacial retreat about 13,000 years ago (Mylroie, 1977). In many vadose canyons throughout the world, examples can be seen where loops or cutoffs have developed along prominent bedding-plane partings exposed in the canyon floor (Fig. 6). As a result, the floor of the upper level coincides with the ceiling of the lower level. The new passage must develop before the parting is bypassed by deepening of the original canyon. This implies that the breakthrough time for the diversion route is virtually nil, allowing the new narrow path to enlarge competitively with the old well-established one. Most such diversions are short.
As the land surface becomes dissected by erosion, patterns of groundwater recharge change. The few large initial water sources may be divided into many smaller ones. Vadose water must travel increasingly greater distances to reach the water table, and extensive complexes of vadose canyons and shafts can form. The resulting pattern of active cave streams is much denser than that of the original surface drainage. Growing dolines eventually form a continuous karst surface. Eventually the only surface streams that retain their flow are the main entrenched rivers and the ephemeral upstream ends of sinking streams.
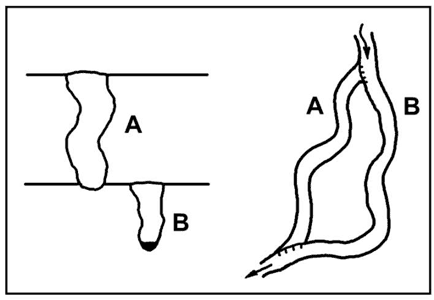
Fig. 6. Stream diversion in an entrenching vadose canyon. The lower loop illustrates nearly zero breakthrough time along the guiding bedding-plane parting, as shown by the minimal entrenchment of segment A below the lower parting. This is a common occurrence, especially in well-bedded carbonates, but it is not a general rule.
The final stage
As the land erodes, the surface intersects underlying cave passages, segmenting them and eventually destroying them entirely. Evidence for the cave may persist for a while as a canyon-like feature or a rubbly zone of collapsed blocks. This final episode in the life of a cave passage usually occupies tens of thousands or even hundreds of thousands of years. However, newer passages continue to develop where the soluble rock extends to lower elevations. In dipping carbonate rocks, new areas of rock are uncovered by erosion at about the same rate as they are eroded away in the up-dip areas. This process ends when the entire soluble rock in the cave region is eroded away.
References
- Audra P. 1994. Karsts alpins; genese des grands reseaux souterrains. Karstologia Memoirs 5, 279 p.
- Berner R.A. and Morse J.W. 1974. Dissolution kinetics of calcium carbonate in sea water; IV: Theory of calcite dissolution. American Journal of Science 274, 108-134.
- Bischoff J.L., Julia R., Shanks W.C. and Rosenbauer R.J. 1994. Karstification without carbonic acid; bedrock dissolution by gypsum-driven dedolomitization. Geology 22/11, 995-998.
- Bocker T. 1969. Karstic water research in Hungary. International Association of Scientific Hydrology Bulletin 14, 4-12.
- Bray L.G. 1972. Preliminary oxidation studies on some cave waters from south Wales. Cave Research Group of Great Britain, Transactions 14, 59-66.
- Clemens T., Huckinghaus D., Sauter M., Liedl R. and Teutsch G. 1997. Simulation of the evolution of maze caves. 12th International Congress of Speleology, and 6th Conference on Limestone Hydrology and Fissured Media, La Chaux-de-Fonds, Switzerland, 2, 65-68.
- Coward J.M.H. 1975. Paleohydrology and streamflow simulation of three karst basins in southeastern West Virginia. Ph.D. dissertation, McMaster University, Hamilton, Ontario, Canada, 394 p.
- Davies W.E. 1960. Origin of caves in folded limestone. National Speleological Society Bulletin 22/1, 5-18.
- Dreybrodt W. 1990. The role of dissolution kinetics in the development of karst aquifers in limestone: a model simulation of karst evolution. Journal of Geology 98/5, 639-655.
- Dreybrodt W. 1996. Principles of early development of karst conduits under natural and man-made conditions revealed by mathematical analysis of numerical models. Water Resources Research 32, 2923-2935.
- Dreybrodt W. and J. Siemers 2000. Cave evolution on two-dimensional networks of primary fractures in limestone. In: Klimchouk A., Ford D., Palmer A. and Dreybrodt W. (Eds.), Speleogenesis: Evolution of Karst Aquifers. Huntsville, Ala.: National Speleological Society, 201-211.
- Ewers R.O. 1982. Cavern development in the dimensions of length and breadth. Ph.D. dissertation, McMaster University, Hamilton, Ontario, 398 p.
- Ford D.C. 1971. Geologic structure and a new explanation of limestone cavern genesis. Transactions of the Cave Research Group of Great Britain 13/2, 81-94.
- Ford D.C. and Ewers R.O. 1978. The development of limestone cave systems in the dimensions of length and depth. Canadian Journal of Earth Sciences 15, 1783-1798.
- Ford D.C., Lauritzen S.-E. and Ewers R.O. 2000. Modeling of initiation and propagation of single conduits and networks. In: Klimchouk A., Ford D., Palmer A. and Dreybrodt W. (Eds.), Speleogenesis: Evolution of Karst Aquifers. Huntsville, Ala., National Speleological Society, 175-183.
- Freeze, R.A., and J.A. Cherry. 1979: Groundwater. Englewood Cliffs, N.J., Prentice-Hall, 604 p.
- Gabrovsek F. 2000. Evolution of early karst aquifers: from simple principles to complex models. Postojna, Slovenia, Institut za razusjivanje krasa ZRC SAZU, 150 p.
- Granger D.E., Fabel D. and Palmer A.N. 2001. Pliocene-Pleistocene incision of the Green River, Kentucky, determined from radioactive decay of 26Al and 10Be in Mammoth Cave sediments. Geological Society of America Bulletin 113/7, 825-836.
- Hauselmann P., Jeannin P.-Y. and Monbaron M. 2001. Relation between alpine paleogeography and cave genesis: the case of the cave system of Sieben Hengste (Berne, Switzerland). In Hauselmann P. and Monbaron M. (Eds.), Cave genesis in the Alpine belt. Proceedings of 1st Workshop for Alpine Speleogenesis, University of Fribourg, Fribourg, Switzerland, 115-123.
- High C.J. 1970. Aspects of the solutional erosion of limestone, with special consideration of lithological factors. Ph.D. dissertation, University of Bristol, Bristol, U.K., 228 p.
- Klimchouk A. and Ford D.C. 2000. Types of karst and evolution of hydrogeologic setting. In: Klimchouk A., Ford D., Palmer A. and Dreybrodt W. (Eds.), Speleogenesis: Evolution of Karst Aquifers. Huntsville, Ala., National Speleological Society, 45-53.
- Lowe D.J. 1992. The origin of limestone caverns: an inception horizon hypothesis. Ph.D. dissertation, Manchester Polytechnic University, U.K., 512 p.
- Meiman J. and Groves C. 1997. Magnitude/ frequency analysis of cave passage development in the Central Kentucky Karst. Proceedings of 6th Annual Mammoth Cave National Park Science Conference, 11-13.
- Mylroie J.E. 1977. Speleogenesis and karst geomorphology of the Helderberg Plateau, Schoharie County, New York. Ph.D. dissertation, Rensselaer Polytechnic Institute, Troy, N.Y., 336 p.
- Palmer A.N. 1972. Dynamics of a sinking stream system, Onesquethaw Cave, New York. National Speleological Society Bulletin 34/3, 89-110.
- Palmer A.N. 1975. The origin of maze caves. National Speleological Society Bulletin 37, 56-76.
- Palmer A.N. 1984. Recent trends in karst geomorphology. Journal of Geological Education 32, 247-253.
- Palmer A.N. 1988. Solutional enlargement of openings in the vicinity of hydraulic structures in karst regions. Dublin, Ohio, Proceedings of 2nd Conference on Environmental Problems in Karst Terranes, Association of Ground Water Scientists and Engineers, 3-13.
- Palmer A.N. 1989. Geomorphic history of the Mammoth Cave System. In W.B. White and E.L. White (eds.), Karst Hydrology: concepts from the Mammoth Cave area. New York, Van Nostrand Reinhold, p. 317-363.
- Palmer A.N. 1991. Origin and morphology of limestone caves. Geological Society of America Bulletin 103, 1-21.
Palmer A.N. 1996. Rates of limestone dissolution and calcite precipitation in cave streams of east-central New York State [abstract]: Northeast Section, Geological Society of America 28/3, 89. - Palmer A.N. 2000. Maze origin by diffuse recharge through overlying formations. In: Klimchouk A., Ford D., Palmer A. and Dreybrodt W. (Eds.), Speleogenesis: Evolution of Karst Aquifers. Huntsville, Ala., National Speleological Society, 387-390.
- Palmer A.N. 2001. Dynamics of cave development by allogenic water. Acta Carsologica 30/2, 13-32.
- Plummer L.N. and Wigley T.M.L. 1976. The dissolution of calcite in CO2-saturated solutions at 25o C and 1 atmosphere total pressure. Geochimica et Cosmochimica Acta 40, 191-202.
- Plummer L.N., Wigley T.M.L. and Parkhurst D.L. 1978. The kinetics of calcite dissolution in CO2-water systems at 5o to 60o C and 0.0 to 1.0 atm CO2. American Journal of Science 278, 179-216.
- Smith D.I. and Newson M.D. 1974. The dynamics of solutional and mechanical erosion in limestone catchments on the Mendip Hills, Somerset. In: Gregory K.J. and Walling D.E. (Eds.), Fluvial processes in instrumented watersheds. Institute of British Geographers, Special Publication 6, 155-167.
- Sweeting M.M. 1950. Erosion cycles and limestone caverns in the Ingleborough District of Yorkshire. Geographical Journal 124, 63-78.
- Vaughan K., Groves C. and Meiman J. 1998. Carbonate chemistry of interstitial fluids within cave stream sediments [abstract]. Conference on Carbon Cycling in Karst, International Geological Correlation Program, Western Kentucky University, Bowling Green, Kentucky, 33-34.
- White W.B. 1977. Role of solution kinetics in the development of karst aquifers. In: Tolson J.S. and Doyle F.L. (Eds.), Karst hydrogeology. International Association of Hydrogeologists, 12th Memoirs, 503-517.
- White W.B. 1984. Rate processes: chemical kinetics and kast landform development. In: LaFleur R.G. (Ed.), Groundwater as a geomorphic agent. Boston, Allen and Unwin, 227-248.